Next: MHD Shocks
Up: Magnetohydrodynamic Fluids
Previous: Nonlinear Tearing Mode Theory
Fast Magnetic Reconnection
Up to now, we have only considered magnetic reconnection that
develops spontaneously from a plasma instability. As we have seen, such reconnection
takes place at a fairly leisurely pace. Let us now consider so-called forced
magnetic reconnection, in which the reconnection takes place as a consequence
of an externally imposed flow, or magnetic perturbation, rather than
occurring spontaneously. The principal difference between forced
and spontaneous reconnection is the development of extremely large, positive
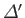 values in the former case. Generally speaking, we expect
values in the former case. Generally speaking, we expect
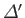 to be
to be
 for spontaneous reconnection. By analogy with the previous
analysis, we would expect forced reconnection to proceed faster than
spontaneous reconnection (because the reconnection rate increases with
increasing
for spontaneous reconnection. By analogy with the previous
analysis, we would expect forced reconnection to proceed faster than
spontaneous reconnection (because the reconnection rate increases with
increasing
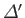 ). The question is--how much faster? To be more
exact, if we take the limit
). The question is--how much faster? To be more
exact, if we take the limit
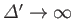 , which
corresponds to the limit of extreme forced reconnection, how fast can we
make the magnetic field reconnect? At present, this is a controversial
question that is far from being completely
resolved. In the following, we shall content
ourselves with a discussion of the two ``classical'' fast reconnection
models. These models form the starting point of virtually all recent research on this
subject (Yamada, Kulsrud, and Ji 2010).
, which
corresponds to the limit of extreme forced reconnection, how fast can we
make the magnetic field reconnect? At present, this is a controversial
question that is far from being completely
resolved. In the following, we shall content
ourselves with a discussion of the two ``classical'' fast reconnection
models. These models form the starting point of virtually all recent research on this
subject (Yamada, Kulsrud, and Ji 2010).
Let us start off by considering the Sweet-Parker model, which was first proposed
by Sweet (Sweet 1958) and
Parker (Parker 1957). The
main features of the envisioned magnetic and plasma flow
fields are illustrated in Figure 7.9. The system is two-dimensional and steady-state (i.e.,
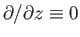 and
and
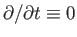 ). The reconnecting magnetic fields are anti-parallel,
and of equal strength,
). The reconnecting magnetic fields are anti-parallel,
and of equal strength, 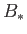 . We imagine that these fields are
being forcibly
pushed together via the action of some external agency.
We expect a strong current sheet to form at the boundary between the
two fields, where the direction of
. We imagine that these fields are
being forcibly
pushed together via the action of some external agency.
We expect a strong current sheet to form at the boundary between the
two fields, where the direction of 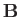 suddenly changes.
This current sheet is assumed to be of thickness
suddenly changes.
This current sheet is assumed to be of thickness
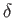 and length
and length 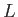 .
.
Figure 7.9:
The Sweet-Parker magnetic reconnection scenario.
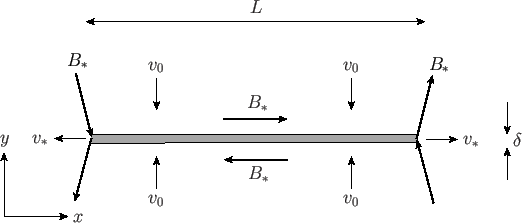 |
Plasma is assumed to diffuse into the current layer, along its whole length,
at some relatively small inflow velocity, 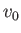 . The plasma is accelerated
along the layer, and eventually expelled from its two ends at some
relatively large exit velocity,
. The plasma is accelerated
along the layer, and eventually expelled from its two ends at some
relatively large exit velocity, 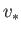 . The inflow velocity
is simply an
. The inflow velocity
is simply an
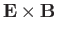 velocity, so
velocity, so
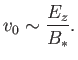 |
(7.225) |
The 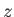 -component of Ohm's law yields
-component of Ohm's law yields
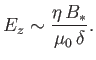 |
(7.226) |
Continuity of plasma flow inside the layer gives
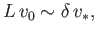 |
(7.227) |
assuming incompressible flow.
Finally, pressure balance along the length of the layer yields
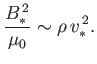 |
(7.228) |
Here, we have balanced the magnetic pressure at the center of the layer
against the dynamic pressure of the outflowing plasma at the ends of the
layer. Note that 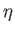 and
and 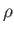 are the plasma resistivity and density,
respectively.
are the plasma resistivity and density,
respectively.
We can measure the rate of reconnection via
the inflow velocity, 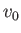 , because all of the magnetic field-lines that are
convected into the layer, with the plasma, are eventually reconnected.
The Alfvén velocity is written
, because all of the magnetic field-lines that are
convected into the layer, with the plasma, are eventually reconnected.
The Alfvén velocity is written
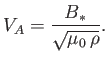 |
(7.229) |
Likewise, we can write the Lundquist number of the plasma as
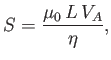 |
(7.230) |
where we have assumed that the length of the reconnecting layer, 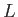 ,
is commensurate with the macroscopic lengthscale of the system.
The reconnection rate is parameterized via the Alfvénic Mach number of
the inflowing plasma, which is defined
,
is commensurate with the macroscopic lengthscale of the system.
The reconnection rate is parameterized via the Alfvénic Mach number of
the inflowing plasma, which is defined
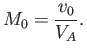 |
(7.231) |
The previous equations can be rearranged to give
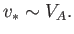 |
(7.232) |
In other words, the plasma is squirted out of the ends of the
reconnecting layer at the Alfvén velocity. Furthermore,
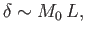 |
(7.233) |
and
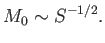 |
(7.234) |
We conclude that the reconnecting layer is extremely
narrow, assuming that the Lundquist number of the plasma is
very large. The magnetic reconnection
takes place on the hybrid timescale
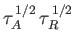 ,
where
,
where 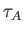 is the Alfvén transit timescale across the
plasma, and
is the Alfvén transit timescale across the
plasma, and 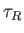 is the resistive diffusion timescale across the
plasma.
is the resistive diffusion timescale across the
plasma.
The Sweet-Parker reconnection ansatz is undoubtedly correct.
It has been simulated numerically many times, and was
confirmed experimentally in the Magnetic Reconnection Experiment (MRX)
operated by Princeton Plasma Physics Laboratory (PPPL) (Ji, Yamada, Hsu, and Kulsrud 1998). The problem is that
Sweet-Parker reconnection takes place far too slowly to account for
many reconnection processes that are thought to take place in the
solar system. For instance, in solar flares
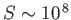 ,
,
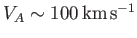 , and
, and
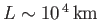 (Priest 1984). According to the
Sweet-Parker model, magnetic energy is released to the plasma via
reconnection on a typical timescale of a few tens of days. In reality,
the energy is released in a few minutes to an hour (Priest 1984). Clearly, we can only hope to
account for solar flares using a reconnection mechanism that operates
far more rapidly than the Sweet-Parker mechanism.
(Priest 1984). According to the
Sweet-Parker model, magnetic energy is released to the plasma via
reconnection on a typical timescale of a few tens of days. In reality,
the energy is released in a few minutes to an hour (Priest 1984). Clearly, we can only hope to
account for solar flares using a reconnection mechanism that operates
far more rapidly than the Sweet-Parker mechanism.
One possible resolution of this problem was suggested by
Petschek (Petschek 1964), who pointed
out that magnetic energy can be converted into plasma thermal energy as a
result of shock waves being set up in the plasma, in addition to the
conversion due to the action of resistive
diffusion. The configuration envisaged by Petschek is sketched in Figure 7.10.
Two waves (slow mode shocks) stand in the flow on either side of the
interface, where the direction of 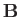 reverses, marking the
boundaries of the plasma outflow regions. A small diffusion region still
exists on the interface, but now constitutes a miniature (in length)
Sweet-Parker system. The width of the reconnecting layer is
given by
reverses, marking the
boundaries of the plasma outflow regions. A small diffusion region still
exists on the interface, but now constitutes a miniature (in length)
Sweet-Parker system. The width of the reconnecting layer is
given by
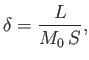 |
(7.235) |
just as in the Sweet-Parker model. However, we do not now assume that the
length, 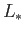 , of the layer is comparable to the characteristic lengthscale,
, of the layer is comparable to the characteristic lengthscale, 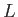 ,
of the system. Rather, the length may be considerably smaller than
,
of the system. Rather, the length may be considerably smaller than 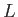 , and
is determined self-consistently from the continuity condition
, and
is determined self-consistently from the continuity condition
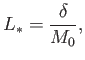 |
(7.236) |
where we have assumed incompressible flow, and an outflow speed of
order the Alfvén speed, as before. Thus, if the inflow speed, 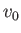 , is
much less than
, is
much less than 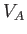 then the length of the reconnecting layer
is much larger than its width, as assumed by Sweet and Parker. On the
other hand, if we allow the inflow velocity to
approach the Alfvén velocity then the layer shrinks in length, so that
then the length of the reconnecting layer
is much larger than its width, as assumed by Sweet and Parker. On the
other hand, if we allow the inflow velocity to
approach the Alfvén velocity then the layer shrinks in length, so that
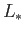 becomes comparable with
becomes comparable with 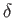 .
.
Figure 7.10:
The Petschek magnetic reconnection scenario.
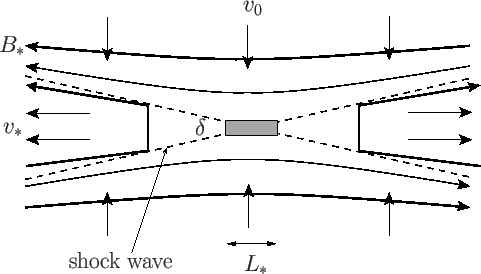 |
It follows that for reasonably large reconnection rates (i.e.,
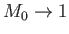 ) the length of the diffusion region becomes much smaller than the characteristic lengthscale
of the system,
) the length of the diffusion region becomes much smaller than the characteristic lengthscale
of the system, 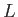 , so that most of the plasma flowing into the
boundary region does so across the standing waves, rather than through the central
diffusion region. The angle
, so that most of the plasma flowing into the
boundary region does so across the standing waves, rather than through the central
diffusion region. The angle 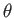 that the shock waves make with
the interface is given approximately
by
that the shock waves make with
the interface is given approximately
by
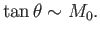 |
(7.237) |
Thus, for small inflow speeds, the outflow is confined to a narrow
wedge along the interface, but as the inflow speed increases, the angle
of the outflow wedges increases to accommodate the increased flow.
It turns out that there is a maximum inflow speed beyond which Petschek-type
solutions cease to exist. The corresponding maximum Alfvénic Mach number,
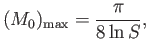 |
(7.238) |
can be regarded as specifying the maximum allowable rate of magnetic
reconnection according to the Petschek model. Clearly, because the maximum reconnection
rate depends inversely on the logarithm of the Lundquist number, rather
than its square root, it is much larger than that predicted by the
Sweet-Parker model.
It must be pointed out that the Petschek model is controversial. Many
researchers think that it is incorrect, and that the maximum
rate of magnetic reconnection allowed by resistive-MHD is that predicted by the
Sweet-Parker model. In particular, Biskamp wrote an influential, and widely quoted, paper reporting the
results of a numerical experiment that appeared to disprove the Petschek
model (Biskamp 1986). When the plasma inflow exceeded that allowed by
the Sweet-Parker model, there was no
acceleration of the reconnection rate. Instead, magnetic flux ``piled up''
in front of the reconnecting layer, and the rate of reconnection never deviated
significantly from that predicted by the Sweet-Parker model. Priest and
Forbes later argued that Biskamp imposed boundary conditions in
his numerical experiment, which precluded Petschek reconnection (Priest and Forbes 1992). Probably
the most powerful argument against the validity of the Petschek model is
the fact that, more than 50 years after it was first proposed, nobody has
ever managed to simulate Petschek reconnection numerically (except by artificially
increasing the resistivity in the reconnecting region--which is not a
legitimate approach) (Yamada, Kulsrud, and Ji 2010).



Next: MHD Shocks
Up: Magnetohydrodynamic Fluids
Previous: Nonlinear Tearing Mode Theory
Richard Fitzpatrick
2016-01-23
![]() and
and
![]() ). The reconnecting magnetic fields are anti-parallel,
and of equal strength,
). The reconnecting magnetic fields are anti-parallel,
and of equal strength, ![]() . We imagine that these fields are
being forcibly
pushed together via the action of some external agency.
We expect a strong current sheet to form at the boundary between the
two fields, where the direction of
. We imagine that these fields are
being forcibly
pushed together via the action of some external agency.
We expect a strong current sheet to form at the boundary between the
two fields, where the direction of ![]() suddenly changes.
This current sheet is assumed to be of thickness
suddenly changes.
This current sheet is assumed to be of thickness
![]() and length
and length ![]() .
.
![]() . The plasma is accelerated
along the layer, and eventually expelled from its two ends at some
relatively large exit velocity,
. The plasma is accelerated
along the layer, and eventually expelled from its two ends at some
relatively large exit velocity, ![]() . The inflow velocity
is simply an
. The inflow velocity
is simply an
![]() velocity, so
velocity, so
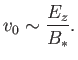
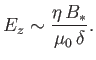
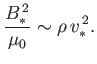
![]() , because all of the magnetic field-lines that are
convected into the layer, with the plasma, are eventually reconnected.
The Alfvén velocity is written
, because all of the magnetic field-lines that are
convected into the layer, with the plasma, are eventually reconnected.
The Alfvén velocity is written
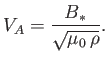
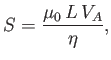
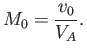
![]() ,
,
![]() , and
, and
![]() (Priest 1984). According to the
Sweet-Parker model, magnetic energy is released to the plasma via
reconnection on a typical timescale of a few tens of days. In reality,
the energy is released in a few minutes to an hour (Priest 1984). Clearly, we can only hope to
account for solar flares using a reconnection mechanism that operates
far more rapidly than the Sweet-Parker mechanism.
(Priest 1984). According to the
Sweet-Parker model, magnetic energy is released to the plasma via
reconnection on a typical timescale of a few tens of days. In reality,
the energy is released in a few minutes to an hour (Priest 1984). Clearly, we can only hope to
account for solar flares using a reconnection mechanism that operates
far more rapidly than the Sweet-Parker mechanism.
![]() reverses, marking the
boundaries of the plasma outflow regions. A small diffusion region still
exists on the interface, but now constitutes a miniature (in length)
Sweet-Parker system. The width of the reconnecting layer is
given by
reverses, marking the
boundaries of the plasma outflow regions. A small diffusion region still
exists on the interface, but now constitutes a miniature (in length)
Sweet-Parker system. The width of the reconnecting layer is
given by
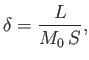
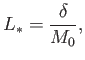
![]() ) the length of the diffusion region becomes much smaller than the characteristic lengthscale
of the system,
) the length of the diffusion region becomes much smaller than the characteristic lengthscale
of the system, ![]() , so that most of the plasma flowing into the
boundary region does so across the standing waves, rather than through the central
diffusion region. The angle
, so that most of the plasma flowing into the
boundary region does so across the standing waves, rather than through the central
diffusion region. The angle ![]() that the shock waves make with
the interface is given approximately
by
that the shock waves make with
the interface is given approximately
by