


Next: Magnetostatics in Magnetic Media
Up: Magnetostatic Fields
Previous: Localized Current Distribution
- Consider two thin current loops. Let loops
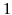 and
and 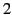 carry the currents
carry the currents 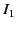 and
and 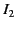 , respectively. The
magnetic force exerted on loop 2 by loop 1 is [see Equation (616)]
, respectively. The
magnetic force exerted on loop 2 by loop 1 is [see Equation (616)]
where
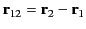 . Here,
. Here, 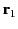 and
and 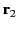 are the position vectors of elements of loops
are the position vectors of elements of loops 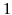 and
and 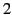 ,
respectively. Demonstrate that the previous expression can also be written
,
respectively. Demonstrate that the previous expression can also be written
Hence, deduce that
in accordance with Newton's third law of motion.
- Consider the two current loops discussed in the previous question. The magnetic field generated at a general position vector
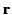 by the
current flowing around loop
by the
current flowing around loop 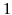 is [see Equation (614)]
is [see Equation (614)]
Demonstrate that
where
Show that the magnetic flux passing through loop 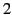 , as a consequence of the current flowing around loop
, as a consequence of the current flowing around loop 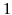 , is
, is
Hence, deduce that the mutual inductance of the two current loops takes the form
- The vector potential of a magnetic dipole of moment
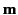 is given by
is given by
Show that the corresponding magnetic field is
- Demonstrate that the torque acting on a magnetic dipole of moment
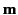 placed in a uniform
external magnetic field
placed in a uniform
external magnetic field 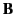 is
is
Hence, deduce that the potential energy of the magnetic dipole is
- Consider two magnetic dipoles,
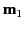 and
and 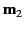 . Suppose
that
. Suppose
that 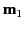 is fixed, whereas
is fixed, whereas 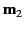 can rotate freely in any direction. Demonstrate that the equilibrium configuration of the second dipole is
such that
can rotate freely in any direction. Demonstrate that the equilibrium configuration of the second dipole is
such that
where 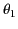 and
and 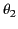 are the angles subtended by
are the angles subtended by 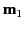 and
and 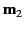 , respectively, with the radius vector joining them.
, respectively, with the radius vector joining them.



Next: Magnetostatics in Magnetic Media
Up: Magnetostatic Fields
Previous: Localized Current Distribution
Richard Fitzpatrick
2014-06-27
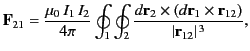
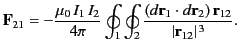
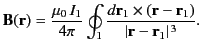
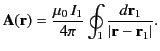
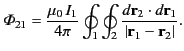
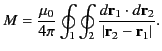
![$\displaystyle {\bf B}({\bf r}) = \frac{\mu_0}{4\pi}\left[\frac{3\,({\bf r}\cdot{\bf m})\,{\bf r}- r^2\,{\bf m}}{r^{\,5}}\right].
$](img1419.png)