Next: Continuous Current Distribution
Up: Magnetostatic Fields
Previous: Introduction
According to the Biot-Savart law, the magnetic field generated at position vector  by a current
by a current 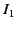 circulating around a thin loop, an element of which is located at position
vector
circulating around a thin loop, an element of which is located at position
vector 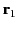 , is
, is
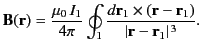 |
(613) |
Suppose that a second current loop carries the current 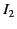 . The net magnetic force exerted on an element,
. The net magnetic force exerted on an element,
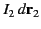 , of this loop, located at position
vector
, of this loop, located at position
vector 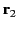 , is
, is
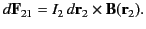 |
(614) |
Hence, the net magnetic force exerted on loop 2 by loop 1 is
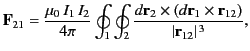 |
(615) |
where
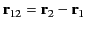 .
.
Richard Fitzpatrick
2014-06-27