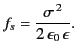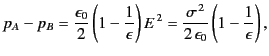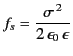Next: Exercises
Up: Electrostatics in Dielectric Media
Previous: Clausius-Mossotti Relation
Consider the behavior of an uncharged dielectric liquid placed in
an electrostatic field. If  is the pressure within the liquid when
in equilibrium with the electrostatic force density
is the pressure within the liquid when
in equilibrium with the electrostatic force density 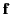 then
force balance requires that
then
force balance requires that
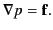 |
(599) |
It follows from Equation (585) that
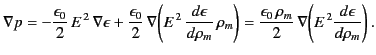 |
(600) |
We can integrate this equation to give
![$\displaystyle \int_{p_1}^{p_2} \frac{dp}{\rho_m} =\frac{\epsilon_0}{2} \left(\l...
...on}{d\rho_m}\right]_2 - \left[E^{\,2}\frac{d\epsilon}{d\rho_m}\right]_1\right),$](img1255.png) |
(601) |
where 1 and 2 refer to two general points in the liquid. Here, it is
assumed that the liquid possesses an equation of state, so that
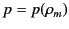 . If the liquid is essentially incompressible
(i.e.,
. If the liquid is essentially incompressible
(i.e.,
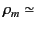 constant) then
constant) then
![$\displaystyle p_2 - p_1 = \frac{\epsilon_0\,\rho_m}{2} \left[E^{\,2}\,\frac{d\epsilon}{d\rho_m} \right]_1^2.$](img1258.png) |
(602) |
Finally, if the liquid obeys the Clausius-Mossotti relation then
![$\displaystyle p_2 - p_1 = \left[ \frac{\epsilon_0\, E^{\,2}}{2} \frac{(\epsilon-1)\,(\epsilon+2)}{3} \right]_{1}^2.$](img1259.png) |
(603) |
According to Equations (554) and (604), if a sphere of dielectric
liquid is placed in a uniform electric field 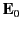 then the
pressure inside the liquid takes the constant value
then the
pressure inside the liquid takes the constant value
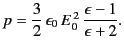 |
(604) |
It is clear that the electrostatic
forces acting on the dielectric are all concentrated at the
edge of the sphere, and are directed radially inwards: that is, the
dielectric is compressed by the external electric field. This
is a somewhat surprising result because the electrostatic forces acting on
a rigid conducting sphere are concentrated at the edge of the sphere, but
are directed radially outwards. We might expect these two cases to give the
same result in the limit
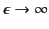 .
The reason that this does not occur is
because a dielectric liquid is
slightly compressible,
and is, therefore, subject to an electrostriction force. There is no
electrostriction force for the case of a completely rigid body.
In fact, the force
density inside a rigid dielectric (for which
.
The reason that this does not occur is
because a dielectric liquid is
slightly compressible,
and is, therefore, subject to an electrostriction force. There is no
electrostriction force for the case of a completely rigid body.
In fact, the force
density inside a rigid dielectric (for which
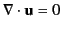 )
is given by Equation (585), with the third term (the electrostriction term)
missing. It is easily demonstrated that the force exerted by an electric
field on a rigid dielectric is directed outwards, and approaches that exerted
on a rigid conductor in the limit
)
is given by Equation (585), with the third term (the electrostriction term)
missing. It is easily demonstrated that the force exerted by an electric
field on a rigid dielectric is directed outwards, and approaches that exerted
on a rigid conductor in the limit
 .
.
As is well known, if a pair of charged (parallel plane) capacitor plates are dipped into
a dielectric liquid then the liquid is drawn up between the plates to
some extent. Let us examine this effect. We can, without loss of
generality, assume that the transition from dielectric to vacuum takes
place in a continuous manner. Consider the electrostatic
pressure difference
between a point  lying just above the surface of the liquid in between the
plates, and a point
lying just above the surface of the liquid in between the
plates, and a point 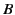 lying just above the surface of the liquid well
away from the capacitor (where
lying just above the surface of the liquid well
away from the capacitor (where  ). The pressure difference is
given by
). The pressure difference is
given by
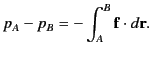 |
(605) |
Note, however, that the Clausius-Mossotti
relation yields
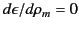 at both
at both  and
and 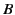 , because
, because
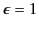 in a vacuum [see Equation (599)]. Thus, it is clear from Equation (585)
that the electrostriction term makes no contribution to the line
integral (606). It follows that
in a vacuum [see Equation (599)]. Thus, it is clear from Equation (585)
that the electrostriction term makes no contribution to the line
integral (606). It follows that
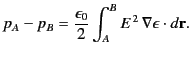 |
(606) |
The only contribution to this integral comes from the vacuum/dielectric
interface in the vicinity of point  (because
(because  is
constant inside the
liquid, and
is
constant inside the
liquid, and  in the vicinity of
point
in the vicinity of
point 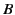 ). Suppose that the electric field
at point
). Suppose that the electric field
at point  has normal and tangential (to the surface) components
has normal and tangential (to the surface) components
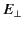 and
and
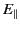 , respectively. Making use of the
boundary conditions that
, respectively. Making use of the
boundary conditions that
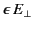 and
and
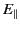 are constant across
a vacuum/dielectric interface, we obtain
are constant across
a vacuum/dielectric interface, we obtain
![$\displaystyle p_A - p_B = \frac{\epsilon_0}{2}\left[ E_\parallel^{\,2}\, (\epsi...
...perp^{\,2}(\epsilon)\, \int_1^\epsilon \frac{d\epsilon}{\epsilon^{\,2}}\right],$](img1272.png) |
(607) |
giving
![$\displaystyle p_A - p_B = \frac{\epsilon_0\,(\epsilon-1)}{2} \left[E_\parallel^{\,2} +\frac{E_\perp^{\,2}}{\epsilon}\right].$](img1273.png) |
(608) |
This electrostatic
pressure difference can be equated to the hydrostatic pressure
difference
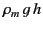 to determine the height,
to determine the height, 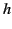 , that the liquid
rises between the plates.
At first sight, the above analysis appears to suggest that
the dielectric liquid is drawn upward by a surface force
acting on the vacuum/dielectric interface in the
region between the plates. In fact, this is far from being the
case. A brief examination of Equation (604) shows that this surface force
is actually directed downwards.
According to Equation (585), the force which causes the liquid to
rise between the plates
is a volume force that develops in the region of non-uniform electric
field at the base of the capacitor, where the field splays out between
the plates. Thus, although we can determine the height to which the fluid
rises between the plates without reference to the electrostriction force,
it is, somewhat paradoxically, this force that is actually
responsible for supporting the liquid against gravity.
, that the liquid
rises between the plates.
At first sight, the above analysis appears to suggest that
the dielectric liquid is drawn upward by a surface force
acting on the vacuum/dielectric interface in the
region between the plates. In fact, this is far from being the
case. A brief examination of Equation (604) shows that this surface force
is actually directed downwards.
According to Equation (585), the force which causes the liquid to
rise between the plates
is a volume force that develops in the region of non-uniform electric
field at the base of the capacitor, where the field splays out between
the plates. Thus, although we can determine the height to which the fluid
rises between the plates without reference to the electrostriction force,
it is, somewhat paradoxically, this force that is actually
responsible for supporting the liquid against gravity.
Let us consider another paradox concerning the electrostatic forces
exerted in a dielectric medium. Suppose that we have two charges
embedded in a uniform dielectric of dielectric constant  . The electric field generated
by each charge is the same as that in a vacuum, except that it is reduced
by a factor
. The electric field generated
by each charge is the same as that in a vacuum, except that it is reduced
by a factor  . We, therefore, expect the force exerted by
one charge on the other to be the same as that in a vacuum, except that it
is also reduced by a factor
. We, therefore, expect the force exerted by
one charge on the other to be the same as that in a vacuum, except that it
is also reduced by a factor  . Let us examine how
this reduction in force comes about. Consider a simple example.
Suppose that we take a parallel plate capacitor, and insert a block
of solid dielectric between the plates. Suppose, further, that there is
a small vacuum gap between the faces of the block and each of
the capacitor plates. Let
. Let us examine how
this reduction in force comes about. Consider a simple example.
Suppose that we take a parallel plate capacitor, and insert a block
of solid dielectric between the plates. Suppose, further, that there is
a small vacuum gap between the faces of the block and each of
the capacitor plates. Let 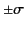 be the surface charge densities
on each of the capacitor plates, and let
be the surface charge densities
on each of the capacitor plates, and let
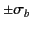 be the bound
charge densities that develop on the outer faces of the intervening dielectric
block. The two layers of bound charge produce equal and opposite
electric fields on each plate, and their effects therefore cancel each other.
Thus, from the point of view of electrical interaction alone there would
appear to be no change in the force exerted by one capacitor plate on the
other
when a dielectric slab is placed between them (assuming that
be the bound
charge densities that develop on the outer faces of the intervening dielectric
block. The two layers of bound charge produce equal and opposite
electric fields on each plate, and their effects therefore cancel each other.
Thus, from the point of view of electrical interaction alone there would
appear to be no change in the force exerted by one capacitor plate on the
other
when a dielectric slab is placed between them (assuming that  remains
constant during this process). That is, the force per unit
area (which is attractive) remains
remains
constant during this process). That is, the force per unit
area (which is attractive) remains
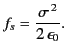 |
(609) |
However, in experiments in which a capacitor is submerged
in a dielectric liquid the force per unit area exerted by one plate
on another is observed to decrease to
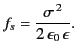 |
(610) |
This apparent paradox can be explained by taking into account the
difference in liquid pressure in the field-filled space
between the plates, and the field-free region outside the capacitor.
This pressure difference is balanced by internal elastic forces in the case
of the solid dielectric discussed earlier, but is transmitted to the
plates in the case of the liquid. We can compute the pressure difference
between a point  on the inside surface of one of the capacitor
plates, and a point
on the inside surface of one of the capacitor
plates, and a point 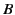 on the outside surface of the same plate using
Equation (607). If we neglect end effects then the electric field is normal
to the plates in the region between the plates, and is zero
everywhere else. Thus, the only contribution to the line integral
(607) comes from the plate/dielectric interface in the vicinity of
point
on the outside surface of the same plate using
Equation (607). If we neglect end effects then the electric field is normal
to the plates in the region between the plates, and is zero
everywhere else. Thus, the only contribution to the line integral
(607) comes from the plate/dielectric interface in the vicinity of
point  . Using Equation (609), we find that
. Using Equation (609), we find that
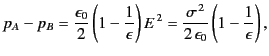 |
(611) |
where 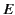 is the normal field-strength between the plates in
the absence of dielectric. The sum of this pressure force and
the purely electrical force (610) yields a net attractive
force per unit area
is the normal field-strength between the plates in
the absence of dielectric. The sum of this pressure force and
the purely electrical force (610) yields a net attractive
force per unit area
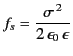 |
(612) |
acting between the plates. Thus, any decrease in the forces exerted
by charges on one another
when they are immersed or embedded in a dielectric medium
can only be understood in terms of mechanical forces transmitted
between these charges by the medium itself.



Next: Exercises
Up: Electrostatics in Dielectric Media
Previous: Clausius-Mossotti Relation
Richard Fitzpatrick
2014-06-27
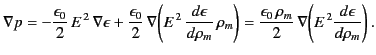
![$\displaystyle \int_{p_1}^{p_2} \frac{dp}{\rho_m} =\frac{\epsilon_0}{2} \left(\l...
...on}{d\rho_m}\right]_2 - \left[E^{\,2}\frac{d\epsilon}{d\rho_m}\right]_1\right),$](img1255.png)
![$\displaystyle p_2 - p_1 = \frac{\epsilon_0\,\rho_m}{2} \left[E^{\,2}\,\frac{d\epsilon}{d\rho_m} \right]_1^2.$](img1258.png)
![]() then the
pressure inside the liquid takes the constant value
then the
pressure inside the liquid takes the constant value
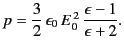
![]() lying just above the surface of the liquid in between the
plates, and a point
lying just above the surface of the liquid in between the
plates, and a point ![]() lying just above the surface of the liquid well
away from the capacitor (where
lying just above the surface of the liquid well
away from the capacitor (where ![]() ). The pressure difference is
given by
). The pressure difference is
given by
![$\displaystyle p_A - p_B = \frac{\epsilon_0}{2}\left[ E_\parallel^{\,2}\, (\epsi...
...perp^{\,2}(\epsilon)\, \int_1^\epsilon \frac{d\epsilon}{\epsilon^{\,2}}\right],$](img1272.png)
![]() . The electric field generated
by each charge is the same as that in a vacuum, except that it is reduced
by a factor
. The electric field generated
by each charge is the same as that in a vacuum, except that it is reduced
by a factor ![]() . We, therefore, expect the force exerted by
one charge on the other to be the same as that in a vacuum, except that it
is also reduced by a factor
. We, therefore, expect the force exerted by
one charge on the other to be the same as that in a vacuum, except that it
is also reduced by a factor ![]() . Let us examine how
this reduction in force comes about. Consider a simple example.
Suppose that we take a parallel plate capacitor, and insert a block
of solid dielectric between the plates. Suppose, further, that there is
a small vacuum gap between the faces of the block and each of
the capacitor plates. Let
. Let us examine how
this reduction in force comes about. Consider a simple example.
Suppose that we take a parallel plate capacitor, and insert a block
of solid dielectric between the plates. Suppose, further, that there is
a small vacuum gap between the faces of the block and each of
the capacitor plates. Let ![]() be the surface charge densities
on each of the capacitor plates, and let
be the surface charge densities
on each of the capacitor plates, and let
![]() be the bound
charge densities that develop on the outer faces of the intervening dielectric
block. The two layers of bound charge produce equal and opposite
electric fields on each plate, and their effects therefore cancel each other.
Thus, from the point of view of electrical interaction alone there would
appear to be no change in the force exerted by one capacitor plate on the
other
when a dielectric slab is placed between them (assuming that
be the bound
charge densities that develop on the outer faces of the intervening dielectric
block. The two layers of bound charge produce equal and opposite
electric fields on each plate, and their effects therefore cancel each other.
Thus, from the point of view of electrical interaction alone there would
appear to be no change in the force exerted by one capacitor plate on the
other
when a dielectric slab is placed between them (assuming that ![]() remains
constant during this process). That is, the force per unit
area (which is attractive) remains
remains
constant during this process). That is, the force per unit
area (which is attractive) remains