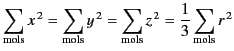Next: Dielectric Liquids in Electrostatic
Up: Electrostatics in Dielectric Media
Previous: Force Density Within Dielectric
Let us now investigate what a dielectric equation of state actually looks like.
Suppose that a dielectric medium is made up of identical molecules that
develop a dipole moment
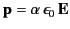 |
(585) |
when placed in an electric field 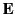 . The constant
. The constant 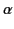 is called
the molecular polarizability. If
is called
the molecular polarizability. If 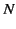 is the number density of
such molecules
then the polarization of the medium is
is the number density of
such molecules
then the polarization of the medium is
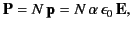 |
(586) |
or
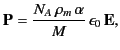 |
(587) |
where 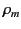 is the mass density,
is the mass density, 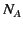 is Avogadro's number, and
is Avogadro's number, and 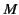 is
the molecular weight. But, how does the electric field experienced
by an individual molecule relate to the average electric field in the
medium? This is not a trivial question because we expect the electric
field to vary strongly (on atomic lengthscales) within the dielectric.
is
the molecular weight. But, how does the electric field experienced
by an individual molecule relate to the average electric field in the
medium? This is not a trivial question because we expect the electric
field to vary strongly (on atomic lengthscales) within the dielectric.
Suppose that the dielectric is polarized by a mean electric field
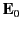 that is uniform (on macroscopic lengthscales), and directed
along the
that is uniform (on macroscopic lengthscales), and directed
along the  -axis. Consider one of the dielectric's constituent molecules. Let us draw a sphere of radius
-axis. Consider one of the dielectric's constituent molecules. Let us draw a sphere of radius  around this particular
molecule. The surface of the sphere is intended to represent the boundary between the microscopic
and the macroscopic ranges of phenomena affecting the molecule. We shall
treat the dielectric outside the sphere as a continuous medium, and the
dielectric inside the sphere as a collection of polarized molecules.
According to Equation (530), there is a bound surface charge of
magnitude
around this particular
molecule. The surface of the sphere is intended to represent the boundary between the microscopic
and the macroscopic ranges of phenomena affecting the molecule. We shall
treat the dielectric outside the sphere as a continuous medium, and the
dielectric inside the sphere as a collection of polarized molecules.
According to Equation (530), there is a bound surface charge of
magnitude
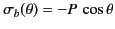 |
(588) |
on the inside of the sphere's surface, where 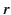 ,
, 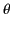 ,
, 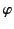 are conventional spherical
coordinates, and
are conventional spherical
coordinates, and
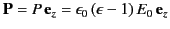 is the uniform polarization of the uniform dielectric outside the sphere. The
magnitude of
is the uniform polarization of the uniform dielectric outside the sphere. The
magnitude of  at the molecule due to this surface charge is
at the molecule due to this surface charge is
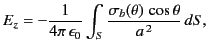 |
(589) |
where
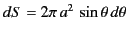 is an element of the surface.
It follows that
is an element of the surface.
It follows that
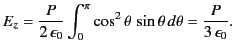 |
(590) |
It is easily demonstrated, from symmetry, that
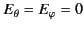 at the molecule.
Thus, the field at the molecule due to the bound charges distributed on the inside of the sphere's surface is
at the molecule.
Thus, the field at the molecule due to the bound charges distributed on the inside of the sphere's surface is
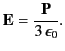 |
(591) |
The field due to the individual molecules within the sphere is
obtained by summing over the dipole fields of these molecules.
The electric field a distance  from a dipole
from a dipole
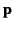 is (see Section 2.7)
is (see Section 2.7)
![$\displaystyle {\bf E} = -\frac{1}{4\pi\,\epsilon_0}\left[\frac{\bf p}{r^{\,3}} - \frac{3\,({\bf p}\cdot{\bf r})\,{\bf r}}{r^{\,5}}\right].$](img1245.png) |
(592) |
It is assumed that the dipole moments of the molecules within the
sphere are all the same, and also that the molecules are evenly distributed
throughout the sphere. This being the case, the value
of  at the molecule due to all of the other molecules
within in the sphere,
at the molecule due to all of the other molecules
within in the sphere,
![$\displaystyle E_z = -\frac{1}{4\pi\,\epsilon_0}\sum_{\rm mols}\left[\frac{ p_z}{r^{\,3}} - \frac{3\,(p_x\, x\,z + p_y\, y\,z + p_z\, z^{\,2})}{r^{\,5}}\right],$](img1246.png) |
(593) |
is zero, because, for evenly distributed molecules,
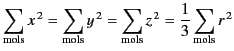 |
(594) |
and
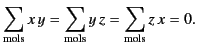 |
(595) |
It is also easily demonstrated that
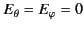 .
Hence, the electric field at the molecule due to the other molecules within
the sphere averages to zero.
.
Hence, the electric field at the molecule due to the other molecules within
the sphere averages to zero.
It is clear that the net electric field experienced by an individual molecule is
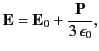 |
(596) |
which is larger than the average electric field,
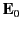 , in the dielectric. The above analysis indicates
that this effect is ascribable to the long range (rather than the short range)
interactions of the molecule with the other molecules in the medium.
Making use of Equation (588), as well as the definition
, in the dielectric. The above analysis indicates
that this effect is ascribable to the long range (rather than the short range)
interactions of the molecule with the other molecules in the medium.
Making use of Equation (588), as well as the definition
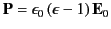 , we obtain
, we obtain
 |
(597) |
which is known as the Clausius-Mossotti relation. This expression is found
to work very well for a wide class of dielectric liquids and
gases. The Clausius-Mossotti relation also yields
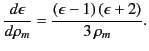 |
(598) |



Next: Dielectric Liquids in Electrostatic
Up: Electrostatics in Dielectric Media
Previous: Force Density Within Dielectric
Richard Fitzpatrick
2014-06-27
![]() that is uniform (on macroscopic lengthscales), and directed
along the
that is uniform (on macroscopic lengthscales), and directed
along the ![]() -axis. Consider one of the dielectric's constituent molecules. Let us draw a sphere of radius
-axis. Consider one of the dielectric's constituent molecules. Let us draw a sphere of radius ![]() around this particular
molecule. The surface of the sphere is intended to represent the boundary between the microscopic
and the macroscopic ranges of phenomena affecting the molecule. We shall
treat the dielectric outside the sphere as a continuous medium, and the
dielectric inside the sphere as a collection of polarized molecules.
According to Equation (530), there is a bound surface charge of
magnitude
around this particular
molecule. The surface of the sphere is intended to represent the boundary between the microscopic
and the macroscopic ranges of phenomena affecting the molecule. We shall
treat the dielectric outside the sphere as a continuous medium, and the
dielectric inside the sphere as a collection of polarized molecules.
According to Equation (530), there is a bound surface charge of
magnitude
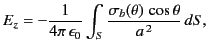
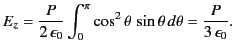
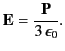
![]() from a dipole
from a dipole
![]() is (see Section 2.7)
is (see Section 2.7)
![$\displaystyle {\bf E} = -\frac{1}{4\pi\,\epsilon_0}\left[\frac{\bf p}{r^{\,3}} - \frac{3\,({\bf p}\cdot{\bf r})\,{\bf r}}{r^{\,5}}\right].$](img1245.png)
![$\displaystyle E_z = -\frac{1}{4\pi\,\epsilon_0}\sum_{\rm mols}\left[\frac{ p_z}{r^{\,3}} - \frac{3\,(p_x\, x\,z + p_y\, y\,z + p_z\, z^{\,2})}{r^{\,5}}\right],$](img1246.png)