


Next: Coulomb's Law
Up: Electrostatic Fields
Previous: Laplace's Equation
Poisson's Equation
Poisson's equation is written
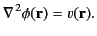 |
(137) |
Here, the function
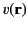 is conventionally referred to as a source.
Suppose that we have to solve Equation (137) over all space, subject to the boundary
condition
is conventionally referred to as a source.
Suppose that we have to solve Equation (137) over all space, subject to the boundary
condition
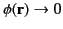 as as 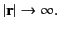 |
(138) |
We can achieve this task by searching for a so-called Green's function,
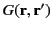 , that satisfies
, that satisfies
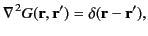 |
(139) |
subject to the boundary condition
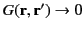 as as 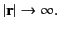 |
(140) |
[Note that the source in Equation (137) is minus the source in the previously defined version of Poisson's equation, (36). Likewise, the Green's function (139) is minus the previously defined Green's function (41). These
differences in sign are purely for the sake of convenience.]
Once we have found the Green's function, the general solution to
Equation (137), subject to the boundary condition (138), is given by
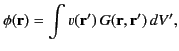 |
(141) |
where the integral is over all space.
We can prove that this expression is indeed a solution to Equation (137) as follows:
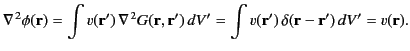 |
(142) |
Here, use has been made of Equations (23) and (24), as well as the fact that 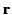 and
and 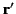 are independent variables.
From Equation (140), the expression for
are independent variables.
From Equation (140), the expression for
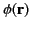 given in Equation (141) satisfies the boundary
condition (138) provided that the volume integral on the right-hand side [of (141)] converges to a finite value.
given in Equation (141) satisfies the boundary
condition (138) provided that the volume integral on the right-hand side [of (141)] converges to a finite value.
According to Equation (25), a solution to Equation (139), subject to the
boundary condition (140), is
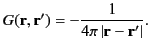 |
(143) |
Actually, we can prove that this is the only solution. Let there be two supposedly different functions,
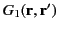 and
and
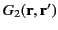 ,
that both satisfy Equation (139), subject to the boundary condition (140). Let us form the difference
,
that both satisfy Equation (139), subject to the boundary condition (140). Let us form the difference
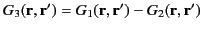 . It follows that
. It follows that
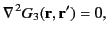 |
(144) |
subject to the boundary condition
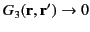 as as 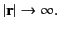 |
(145) |
However, as we saw in Section 2.2, the only solution to the previous two equations is
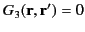 |
(146) |
for all 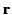 (and
(and 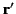 ).
Hence, the functions
).
Hence, the functions
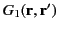 and
and
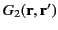 are identical, and the Green's function (143) is unique. It follows from Equation (141)
that the general solution to Poisson's equation, (137), subject to the boundary condition (138), is
are identical, and the Green's function (143) is unique. It follows from Equation (141)
that the general solution to Poisson's equation, (137), subject to the boundary condition (138), is
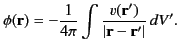 |
(147) |
Furthermore, this solution is unique.



Next: Coulomb's Law
Up: Electrostatic Fields
Previous: Laplace's Equation
Richard Fitzpatrick
2014-06-27