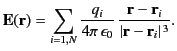Next: Electric Scalar Potential
Up: Electrostatic Fields
Previous: Poisson's Equation
Coulomb's Law
Coulomb's law is equivalent to the statement that the electric field
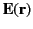 generated by a point charge
generated by a point charge  located at
located at
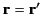 is
is
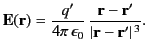 |
(148) |
The electric force 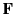 exerted on a point charge
exerted on a point charge 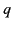 located at position vector
located at position vector  is
is
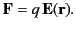 |
(149) |
Hence,
 |
(150) |
It follows that the electrostatic force acting between two point charges is inverse-square, central, proportional to the product of the charges, and repulsive if
both charges are of the same sign.
Electric fields are superposable (see Section 1.2), which means that the electric field generated by 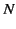 point charges,
point charges, 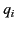 , located at
position vectors
, located at
position vectors 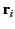 , for
, for 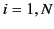 , is
, is
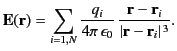 |
(151) |
In the continuum limit, the previous expression
becomes
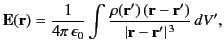 |
(152) |
where
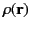 is the charge density (i.e., the electric charge per unit volume), and the integral is
over all space.
is the charge density (i.e., the electric charge per unit volume), and the integral is
over all space.



Next: Electric Scalar Potential
Up: Electrostatic Fields
Previous: Poisson's Equation
Richard Fitzpatrick
2014-06-27
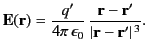
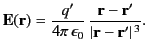

![]() point charges,
point charges, ![]() , located at
position vectors
, located at
position vectors ![]() , for
, for ![]() , is
, is