


Next: Poisson's Equation
Up: Electrostatic Fields
Previous: Introduction
Laplace's Equation
Laplace's equation is written
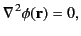 |
(127) |
where the function
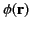 is often referred to as a potential. Suppose that we wish to find a
solution to this equation in some finite volume
is often referred to as a potential. Suppose that we wish to find a
solution to this equation in some finite volume  , bounded by a closed surface
, bounded by a closed surface  ,
subject to the boundary condition
,
subject to the boundary condition
 |
(128) |
when  lies on
lies on  .
Consider the vector identity
.
Consider the vector identity
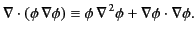 |
(129) |
Integrating this expression over  , making use of the divergence theorem, we obtain
, making use of the divergence theorem, we obtain
 |
(130) |
It follows from Equations (127) and (128) that
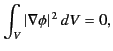 |
(131) |
which implies that
 throughout
throughout  and on
and on  . Hence, Equation (128) yields
. Hence, Equation (128) yields
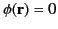 |
(132) |
throughout  and on
and on  . We conclude that the only solution to Laplace's equation, (127), subject to the boundary condition (128), is
the trivial solution (132). Finally, if we let the surface
. We conclude that the only solution to Laplace's equation, (127), subject to the boundary condition (128), is
the trivial solution (132). Finally, if we let the surface  tend to infinity then we deduce that the only
solution to Laplace's equation, (127), subject to the boundary condition
tend to infinity then we deduce that the only
solution to Laplace's equation, (127), subject to the boundary condition
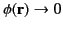 as as 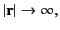 |
(133) |
is
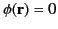 |
(134) |
for all  .
.
Consider a potential
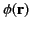 that satisfies Laplace's equation, (127), in some finite volume
that satisfies Laplace's equation, (127), in some finite volume  , bounded by the closed surface
, bounded by the closed surface  ,
subject to the boundary condition
,
subject to the boundary condition
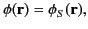 |
(135) |
when  lies on
lies on  . Here,
. Here,
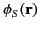 is a known surface distribution. We can demonstrate that this potential is unique.
Let
is a known surface distribution. We can demonstrate that this potential is unique.
Let
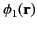 and
and
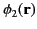 be two supposedly different potentials that both satisfy Laplace's equation throughout
be two supposedly different potentials that both satisfy Laplace's equation throughout  ,
as well as the previous boundary condition on
,
as well as the previous boundary condition on  . Let us form the difference
. Let us form the difference
 .
This function satisfies Laplace's equation throughout
.
This function satisfies Laplace's equation throughout  , subject to the boundary condition
, subject to the boundary condition
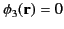 |
(136) |
when  lies on
lies on  .
However, as we have already seen, this implies that
.
However, as we have already seen, this implies that
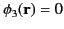 throughout
throughout  and on
and on  . Hence,
. Hence,
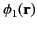 and
and
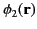 are identical, and
the potential
are identical, and
the potential
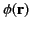 is therefore unique.
is therefore unique.



Next: Poisson's Equation
Up: Electrostatic Fields
Previous: Introduction
Richard Fitzpatrick
2014-06-27
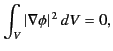
![]() that satisfies Laplace's equation, (127), in some finite volume
that satisfies Laplace's equation, (127), in some finite volume ![]() , bounded by the closed surface
, bounded by the closed surface ![]() ,
subject to the boundary condition
,
subject to the boundary condition