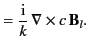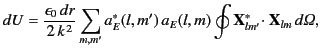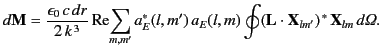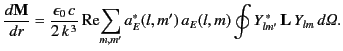Next: Solution of Inhomogeneous Helmholtz
Up: Multipole Expansion
Previous: Multipole Expansion of Vector
Let us examine some of the properties of the multipole fields (1470)-(1471) and (1474)-(1475). Consider, first of all,
the so-called near zone, in which 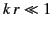 .
In this region,
.
In this region, 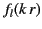 is dominated by
is dominated by 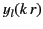 , which blows up as
, which blows up as
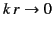 , and which has the asymptotic
expansion (1429), unless the coefficient of
, and which has the asymptotic
expansion (1429), unless the coefficient of 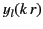 vanishes identically. Excluding this
possibility, the limiting behavior of the magnetic field for an
electric
vanishes identically. Excluding this
possibility, the limiting behavior of the magnetic field for an
electric 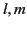 multipole is
multipole is
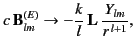 |
(1483) |
where the proportionality constant is chosen for later convenience. To
find the corresponding electric field, we must take the curl of the right-hand side of the above equation.
The following operator identity is useful
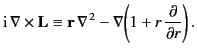 |
(1484) |
The electric field (1475) can be written
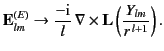 |
(1485) |
Because
 is a solution of Laplace's equation, it is annihilated by the first term on the right-hand side of
(1486). Consequently, for
an electric
is a solution of Laplace's equation, it is annihilated by the first term on the right-hand side of
(1486). Consequently, for
an electric 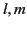 multipole, the electric field in the near zone becomes
multipole, the electric field in the near zone becomes
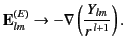 |
(1486) |
This, of course, is an electrostatic multipole field. Such a field can be obtained
in a more straightforward manner by observing that
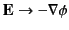 , where
, where
 , in the near zone. Solving Laplace's
equation by separation of variables in spherical coordinates, and
demanding that
, in the near zone. Solving Laplace's
equation by separation of variables in spherical coordinates, and
demanding that 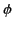 be well behaved as
be well behaved as
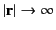 ,
yields
,
yields
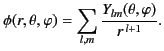 |
(1487) |
Note that (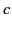 times) the magnetic field (1485) is smaller than the electric field
(1488) by a factor of order
times) the magnetic field (1485) is smaller than the electric field
(1488) by a factor of order  . Thus, in the near zone, (
. Thus, in the near zone, (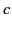 times) the magnetic
field associated with an electric multipole is much smaller
than the corresponding electric field. For magnetic multipole fields, it
is evident from Equations (1470)-(1471) and (1474)-(1475) that the roles of
times) the magnetic
field associated with an electric multipole is much smaller
than the corresponding electric field. For magnetic multipole fields, it
is evident from Equations (1470)-(1471) and (1474)-(1475) that the roles of
 and
and
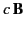 are interchanged according to the transformation
are interchanged according to the transformation
In the so-called far zone, or radiation zone, in which
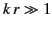 , the multipole fields depend on the boundary conditions
imposed at infinity. For definiteness, let us consider the case of
outgoing waves at infinity, which is appropriate to radiation
by a localized source. For this case, the radial function
, the multipole fields depend on the boundary conditions
imposed at infinity. For definiteness, let us consider the case of
outgoing waves at infinity, which is appropriate to radiation
by a localized source. For this case, the radial function
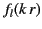 contains only the spherical Hankel function
contains only the spherical Hankel function
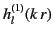 .
From the asymptotic form (1432), it is clear that in the radiation zone
the magnetic field of an electric
.
From the asymptotic form (1432), it is clear that in the radiation zone
the magnetic field of an electric 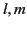 multipole varies as
multipole varies as
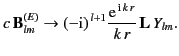 |
(1490) |
Using Equation (1475), the corresponding electric field can be written
![$\displaystyle {\bf E}_{lm}^{(E)} = \frac{(-{\rm i})^{\,l}}{k^{\,2}}\left[\nabla...
...} +\frac{{\rm e}^{\,{\rm i}\,k\,r}}{r} \,\nabla\times {\bf L} \,Y_{lm} \right].$](img3146.png) |
(1491) |
Neglecting terms that fall off faster than 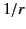 , the above expression
reduces to
, the above expression
reduces to
![$\displaystyle {\bf E}_{lm}^{(E)} = -(-{\rm i})^{\,l+1} \frac{{\rm e}^{\,{\rm i}...
...\times {\bf L}\,Y_{lm}-\frac{1}{k}({\bf r}\,\nabla^{\,2}-\nabla) Y_{lm}\right],$](img3147.png) |
(1492) |
where use has been made of the identity (1486), and
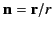 is a unit vector pointing
in the radial direction. The second term in square brackets
is smaller than the first term by a factor of order
is a unit vector pointing
in the radial direction. The second term in square brackets
is smaller than the first term by a factor of order 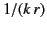 , and can, therefore, be neglected in the limit
, and can, therefore, be neglected in the limit 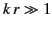 . Thus, we find that the electric
field in the radiation zone takes the form
. Thus, we find that the electric
field in the radiation zone takes the form
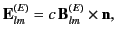 |
(1493) |
where
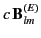 is given by Equation (1492). These fields are typical
radiation fields: that is, they are transverse to the radius vector,
mutually orthogonal, fall off like
is given by Equation (1492). These fields are typical
radiation fields: that is, they are transverse to the radius vector,
mutually orthogonal, fall off like 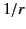 , and are such that
, and are such that
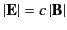 . To obtain expansions for magnetic multipoles,
we merely make the transformation (1490)-(1491).
. To obtain expansions for magnetic multipoles,
we merely make the transformation (1490)-(1491).
Consider a linear superposition of electric 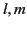 multipoles with
different
multipoles with
different  values that all possess a common
values that all possess a common  value. Suppose that
all multipoles correspond to outgoing waves at infinity. It follows
from Equations (1474)-(1476) that
value. Suppose that
all multipoles correspond to outgoing waves at infinity. It follows
from Equations (1474)-(1476) that
For harmonically varying fields, the time-averaged energy density is
given by
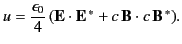 |
(1496) |
In the radiation zone, the two terms on the right-hand side of the above equation are equal.
It follows that the energy contained in a spherical shell
lying between radii 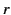 and
and 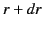 is
is
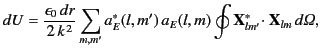 |
(1497) |
where use has been made of the asymptotic form (1432) of the spherical Hankel function
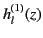 .
The orthogonality relation (1477) leads to
.
The orthogonality relation (1477) leads to
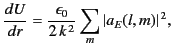 |
(1498) |
which is clearly independent of the radius. For a general superposition
of electric and magnetic multipoles, the sum over  becomes a sum
over
becomes a sum
over  and
and  , whereas
, whereas
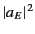 becomes
becomes
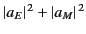 .
Thus, the net
energy in a spherical shell situated in the radiation zone is an
incoherent sum over all multipoles.
.
Thus, the net
energy in a spherical shell situated in the radiation zone is an
incoherent sum over all multipoles.
The time-averaged angular momentum density of harmonically varying
electromagnetic fields is given by
![$\displaystyle {\bf m} = \frac{\epsilon_0}{2}\, {\rm Re}\, [{\bf r}\times({\bf E}\times {\bf B}^{\,\ast})].$](img3162.png) |
(1499) |
For a superposition of electric multipoles, the triple product can
be expanded, and the electric field (1497) substituted, to
give
![$\displaystyle {\bf m} = \frac{\epsilon_0 \,c}{2\,k} \,{\rm Re}\,[{\bf B}^{\,\ast}({\bf L}\cdot {\bf B})].$](img3163.png) |
(1500) |
Thus, the net angular momentum contained in a spherical shell lying between radii 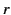 and
and 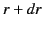 (in the radiation zone) is
(in the radiation zone) is
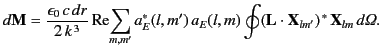 |
(1501) |
It follows from Equations (1436) and (1476) that
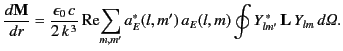 |
(1502) |
According to Equations (1439)-(1441), the Cartesian components of
 can be written:
can be written:
Thus, for a general  th order electric multipole that consists of
a superposition of different
th order electric multipole that consists of
a superposition of different  values, only the
values, only the  component of
the
angular momentum takes a relatively simple form.
component of
the
angular momentum takes a relatively simple form.



Next: Solution of Inhomogeneous Helmholtz
Up: Multipole Expansion
Previous: Multipole Expansion of Vector
Richard Fitzpatrick
2014-06-27
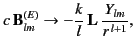
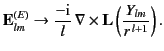
![]() , the multipole fields depend on the boundary conditions
imposed at infinity. For definiteness, let us consider the case of
outgoing waves at infinity, which is appropriate to radiation
by a localized source. For this case, the radial function
, the multipole fields depend on the boundary conditions
imposed at infinity. For definiteness, let us consider the case of
outgoing waves at infinity, which is appropriate to radiation
by a localized source. For this case, the radial function
![]() contains only the spherical Hankel function
contains only the spherical Hankel function
![]() .
From the asymptotic form (1432), it is clear that in the radiation zone
the magnetic field of an electric
.
From the asymptotic form (1432), it is clear that in the radiation zone
the magnetic field of an electric ![]() multipole varies as
multipole varies as
![$\displaystyle {\bf E}_{lm}^{(E)} = \frac{(-{\rm i})^{\,l}}{k^{\,2}}\left[\nabla...
...} +\frac{{\rm e}^{\,{\rm i}\,k\,r}}{r} \,\nabla\times {\bf L} \,Y_{lm} \right].$](img3146.png)
![$\displaystyle {\bf E}_{lm}^{(E)} = -(-{\rm i})^{\,l+1} \frac{{\rm e}^{\,{\rm i}...
...\times {\bf L}\,Y_{lm}-\frac{1}{k}({\bf r}\,\nabla^{\,2}-\nabla) Y_{lm}\right],$](img3147.png)
![]() multipoles with
different
multipoles with
different ![]() values that all possess a common
values that all possess a common ![]() value. Suppose that
all multipoles correspond to outgoing waves at infinity. It follows
from Equations (1474)-(1476) that
value. Suppose that
all multipoles correspond to outgoing waves at infinity. It follows
from Equations (1474)-(1476) that