Next: Multipole Expansion of Vector
Up: Multipole Expansion
Previous: Multipole Expansion of Scalar
Angular Momentum Operators
It is well known from quantum mechanics that Equation (1417) can be written
in the form
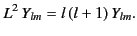 |
(1434) |
Here, the differential operator 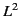 is given by
is given by
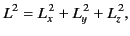 |
(1435) |
where
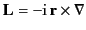 |
(1436) |
is 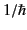 times the orbital angular momentum operator of
wave mechanics.
times the orbital angular momentum operator of
wave mechanics.
The components of 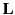 are conveniently written in the combinations
are conveniently written in the combinations
Note that 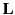 only operates on angular variables, and is independent
of
only operates on angular variables, and is independent
of 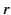 . It is evident from the definition (1438)
that
. It is evident from the definition (1438)
that
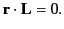 |
(1440) |
It is easily
demonstrated from Equations (1439)-(1441) that
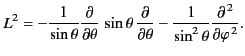 |
(1441) |
The following results are well known in quantum mechanics:
In addition,
where
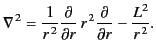 |
(1448) |



Next: Multipole Expansion of Vector
Up: Multipole Expansion
Previous: Multipole Expansion of Scalar
Richard Fitzpatrick
2014-06-27
![]() are conveniently written in the combinations
are conveniently written in the combinations