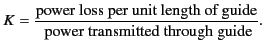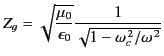Next: Dielectric Waveguides
Up: Resonant Cavities and Waveguides
Previous: Cylindrical Cavities
Let us consider the transmission of electromagnetic waves along the
axis of a waveguide, which is simply a long, axially symmetric, hollow
conductor with open ends. In order to represent a wave propagating along
the  -direction,
we express the dependence of field quantities on the spatial coordinates
and time in the form
-direction,
we express the dependence of field quantities on the spatial coordinates
and time in the form
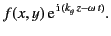 |
(1354) |
The guide propagation constant,  , is just the
, is just the
 of previous sections, except that it is no longer restricted
by the boundary conditions to take discrete values. The general considerations
of Section 10.5 still apply, so that we can treat TM and TE modes separately.
The solutions for
of previous sections, except that it is no longer restricted
by the boundary conditions to take discrete values. The general considerations
of Section 10.5 still apply, so that we can treat TM and TE modes separately.
The solutions for  are identical to those for axially symmetric cavities
already discussed. Although
are identical to those for axially symmetric cavities
already discussed. Although  is not restricted in magnitude,
we note that for every eigenvalue of the transverse wave equation,
is not restricted in magnitude,
we note that for every eigenvalue of the transverse wave equation,
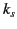 , there is
a lowest value of
, there is
a lowest value of 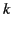 , namely
, namely 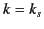 (often designated
(often designated 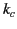 for waveguides), for which
for waveguides), for which
 is real.
This corresponds to the cutoff frequency, below which waves are
not transmitted by the mode in question, and the fields fall off exponentially
with increasing
is real.
This corresponds to the cutoff frequency, below which waves are
not transmitted by the mode in question, and the fields fall off exponentially
with increasing  . In fact, the waveguide dispersion relation for
a particular mode can easily be shown to take the form
. In fact, the waveguide dispersion relation for
a particular mode can easily be shown to take the form
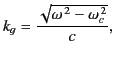 |
(1355) |
where
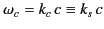 |
(1356) |
is the cutoff frequency. There is an absolute cutoff frequency associated
with the mode of lowest frequency: that is, the mode with the
lowest value
of 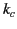 .
.
For real  (i.e.,
(i.e.,
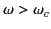 ), it is clear from Equation (1357) that the wave propagates
along the guide at the phase velocity
), it is clear from Equation (1357) that the wave propagates
along the guide at the phase velocity
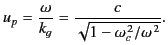 |
(1357) |
It is evident that this velocity is greater than that of electromagnetic
waves in free space.
The velocity is not constant, however, but depends on the frequency.
The waveguide thus behaves as a dispersive medium. The group
velocity of a wave pulse propagated along the guide is given by
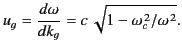 |
(1358) |
It can be seen that 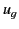 is always smaller than
is always smaller than 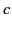 , and also that
, and also that
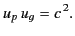 |
(1359) |
For a TM mode (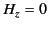 ), Equations (1342)-(1343) yield
), Equations (1342)-(1343) yield
where use has been made of
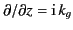 .
For TE modes (
.
For TE modes (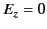 ), Equations (1344)-(1345) give
), Equations (1344)-(1345) give
The time-average  component of the Poynting vector,
component of the Poynting vector, 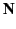 , is
given by
, is
given by
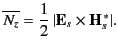 |
(1364) |
It follows that
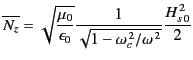 |
(1365) |
for TE modes, and
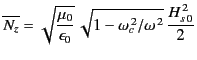 |
(1366) |
for TM modes. The subscript 0 denotes the peak value of a wave quantity.
For a given mode, waveguide losses can be estimated by integrating Equation (1319) over the
wall of the guide. The energy flow of
a propagating wave attenuates as
 , where
, where
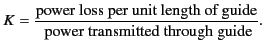 |
(1367) |
Thus,
 |
(1368) |
where the numerator is integrated over unit length of the wall, and the denominator
is integrated over the transverse cross-section of the guide. It is
customary to define the guide impedance, 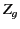 , by writing
, by writing
 |
(1369) |
Here, both integrals are over the transverse cross-section of the guide.
It follows from Equations (1366) and (1367) that
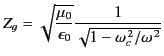 |
(1370) |
for TE modes, and
 |
(1371) |
for TM modes. For both types of mode,
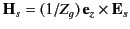 .
.



Next: Dielectric Waveguides
Up: Resonant Cavities and Waveguides
Previous: Cylindrical Cavities
Richard Fitzpatrick
2014-06-27
![]() (i.e.,
(i.e.,
![]() ), it is clear from Equation (1357) that the wave propagates
along the guide at the phase velocity
), it is clear from Equation (1357) that the wave propagates
along the guide at the phase velocity
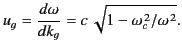
![]() ), Equations (1342)-(1343) yield
), Equations (1342)-(1343) yield
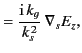
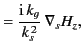
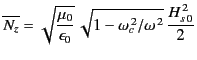
![]() , where
, where