Next: Waveguides
Up: Resonant Cavities and Waveguides
Previous: Axially Symmetric Cavities
Let us apply the methods of the previous section to the TM modes of a
right circular cylinder of radius 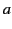 . We can write
. We can write
 |
(1344) |
where
 satisfies the equation
satisfies the equation
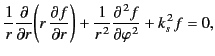 |
(1345) |
and 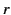 ,
, 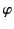 ,
,  are cylindrical coordinates. Let
are cylindrical coordinates. Let
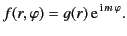 |
(1346) |
It follows that
 |
(1347) |
or
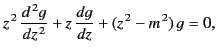 |
(1348) |
where 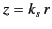 . The above equation can be recognized as Bessel's
equation. The independent solutions of this equation
are denoted
. The above equation can be recognized as Bessel's
equation. The independent solutions of this equation
are denoted 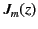 and
and 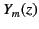 . The
. The 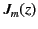 are regular at
are regular at 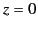 , whereas
the
, whereas
the 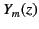 are singular. Moreover, both solutions are regular at large
are singular. Moreover, both solutions are regular at large 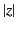 .
.
Because the axis (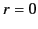 ) lies within the cavity, the radial eigenfunction
must be regular at
) lies within the cavity, the radial eigenfunction
must be regular at 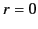 . This immediately rules out the
. This immediately rules out the
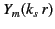 solutions. Thus, the most general solution for a TM mode is
solutions. Thus, the most general solution for a TM mode is
 |
(1349) |
The 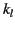 are the eigenvalues of
are the eigenvalues of 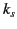 , and are determined by the
solution of
, and are determined by the
solution of
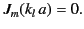 |
(1350) |
The above constraint ensures that the tangential electric field is zero
on the conducting walls surrounding the cavity ( ).
).
The most general solution for a TE mode is
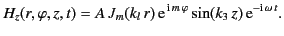 |
(1351) |
In this case, the 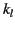 are determined by the solution
of
are determined by the solution
of
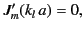 |
(1352) |
where  denotes differentiation with respect to argument.
The above constraint ensures that the normal magnetic field is
zero on the conducting walls surrounding the cavity. The oscillation
frequencies of both TM and TE modes are given by
denotes differentiation with respect to argument.
The above constraint ensures that the normal magnetic field is
zero on the conducting walls surrounding the cavity. The oscillation
frequencies of both TM and TE modes are given by
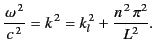 |
(1353) |
If  is the ordinal number of a zero of a particular Bessel function
of order
is the ordinal number of a zero of a particular Bessel function
of order  (defined such that
(defined such that  increases with increasing values of the argument) then
each mode is characterized by three integers,
increases with increasing values of the argument) then
each mode is characterized by three integers,  ,
,  ,
,  , as in the
rectangular case. The
, as in the
rectangular case. The  th zero of
th zero of 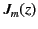 is conventionally denoted
is conventionally denoted
 [so,
[so,
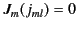 ]. Likewise, the
]. Likewise, the  th zero of
th zero of
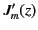 is denoted
is denoted 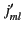 . Table 2 shows the first few
zeros of
. Table 2 shows the first few
zeros of 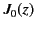 ,
,  ,
,  , and
, and 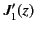 . It is clear that,
for fixed
. It is clear that,
for fixed  and
and  , the lowest frequency mode (i.e., the mode
with the lowest value of
, the lowest frequency mode (i.e., the mode
with the lowest value of 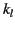 ) is a TE mode. The mode with the
next highest frequency is a TM mode. The next highest frequency
mode is a TE mode, and so on.
) is a TE mode. The mode with the
next highest frequency is a TM mode. The next highest frequency
mode is a TE mode, and so on.
Table:
The first few values of 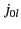 ,
, 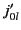 ,
, 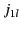 and
and 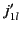 .
.

|
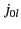
|
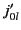
|
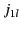
|
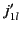
|
| 1 |
2.4048 |
0.0000 |
3.8317 |
1.8412 |
| 2 |
5.5201 |
3.8317 |
7.0156 |
5.3314 |
| 3 |
8.6537 |
7.0156 |
10.173 |
8.5363 |
| 4 |
11.792 |
10.173 |
13.324 |
11.706 |
|



Next: Waveguides
Up: Resonant Cavities and Waveguides
Previous: Axially Symmetric Cavities
Richard Fitzpatrick
2014-06-27
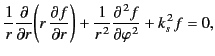

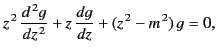
![]() ) lies within the cavity, the radial eigenfunction
must be regular at
) lies within the cavity, the radial eigenfunction
must be regular at ![]() . This immediately rules out the
. This immediately rules out the
![]() solutions. Thus, the most general solution for a TM mode is
solutions. Thus, the most general solution for a TM mode is