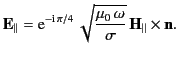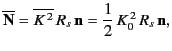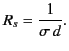Next: Quality Factor of a
Up: Resonant Cavities and Waveguides
Previous: Boundary Conditions
Consider a rectangular vacuum region totally enclosed by conducting
walls. In this case, all of the field components satisfy the wave equation
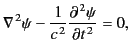 |
(1307) |
where 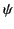 represents any component of
represents any component of  or
or  . The
boundary conditions (1302)-(1305) require that the electric field at the boundary be
normal to the conducting walls, whereas the magnetic field be tangential.
If
. The
boundary conditions (1302)-(1305) require that the electric field at the boundary be
normal to the conducting walls, whereas the magnetic field be tangential.
If 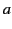 ,
,  , and
, and 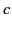 are the dimensions of the cavity, in the
are the dimensions of the cavity, in the  ,
, 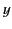 , and
, and  directions, respectively, then it
is readily verified that the electric field components are
directions, respectively, then it
is readily verified that the electric field components are
where
Here,  ,
,  ,
,  are non-negative integers. The allowed frequencies are given by
are non-negative integers. The allowed frequencies are given by
 |
(1314) |
It is clear from Equations (1310)-(1312) that at least two of the integers
 ,
,  ,
,  must be different from zero in order to have non-vanishing
fields.
The magnetic fields, obtained by solving
must be different from zero in order to have non-vanishing
fields.
The magnetic fields, obtained by solving
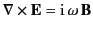 , automatically satisfy the appropriate boundary conditions, and
are in phase quadrature with the corresponding electric fields. Thus, the
sum of the total electric and magnetic energies within the cavity is
constant, although the two terms oscillate separately.
, automatically satisfy the appropriate boundary conditions, and
are in phase quadrature with the corresponding electric fields. Thus, the
sum of the total electric and magnetic energies within the cavity is
constant, although the two terms oscillate separately.
The amplitudes of the electric field components are not independent,
but are related by the divergence condition
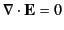 ,
which yields
,
which yields
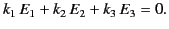 |
(1315) |
There are, in general, two linearly independent vectors  that
satisfy this condition, corresponding to two different polarizations. (The
exception is when one of the integers
that
satisfy this condition, corresponding to two different polarizations. (The
exception is when one of the integers  ,
,  ,
,  is zero,
in which case
is zero,
in which case  is fixed in direction.) Each electric field vector is accompanied by
a perpendicular magnetic field vector. The fields corresponding to a given
set of integers
is fixed in direction.) Each electric field vector is accompanied by
a perpendicular magnetic field vector. The fields corresponding to a given
set of integers  ,
,  , and
, and  constitute a
particular mode of oscillation
of the cavity. It is evident from standard Fourier theory that the different
modes are orthogonal (i.e., they are normal modes), and that
they form a complete set. In other words, any general electric and
magnetic fields that satisfy the boundary conditions (1302)-(1305) can be
unambiguously decomposed into some
linear combination of all of the various possible normal modes of the
cavity. Because each normal mode oscillates at a specific frequency,
it is clear that if we are given the electric and magnetic fields inside
the cavity at time
constitute a
particular mode of oscillation
of the cavity. It is evident from standard Fourier theory that the different
modes are orthogonal (i.e., they are normal modes), and that
they form a complete set. In other words, any general electric and
magnetic fields that satisfy the boundary conditions (1302)-(1305) can be
unambiguously decomposed into some
linear combination of all of the various possible normal modes of the
cavity. Because each normal mode oscillates at a specific frequency,
it is clear that if we are given the electric and magnetic fields inside
the cavity at time 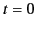 then the subsequent behavior of the fields
is uniquely determined for all time.
then the subsequent behavior of the fields
is uniquely determined for all time.
The conducting walls gradually absorb energy from the cavity, due to
their finite resistivity, at a rate that can easily be calculated.
For finite 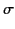 , the small tangential component of
, the small tangential component of  at
the walls can be estimated using Equation (1306):
at
the walls can be estimated using Equation (1306):
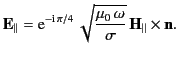 |
(1316) |
Now, the tangential component of  at the walls is slightly
different from that given by the ideal solution. However, this
is a small effect, and can be neglected to leading order in
at the walls is slightly
different from that given by the ideal solution. However, this
is a small effect, and can be neglected to leading order in
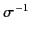 .
The time averaged energy flux into the walls is then given by
.
The time averaged energy flux into the walls is then given by
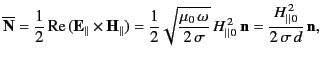 |
(1317) |
where
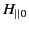 is the peak value of the tangential
magnetic field at the walls that is
predicted by the ideal solution. According to the boundary condition (1305),
is the peak value of the tangential
magnetic field at the walls that is
predicted by the ideal solution. According to the boundary condition (1305),
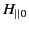 is equal to the peak value of the surface current
density
is equal to the peak value of the surface current
density 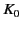 . It is helpful to define a surface resistance,
. It is helpful to define a surface resistance,
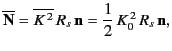 |
(1318) |
where
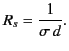 |
(1319) |
This approach makes it clear that the dissipation of energy in a resonant cavity is due
to ohmic heating in a thin layer, whose thickness is of order the
skin depth, covering the surface of the conducting walls.



Next: Quality Factor of a
Up: Resonant Cavities and Waveguides
Previous: Boundary Conditions
Richard Fitzpatrick
2014-06-27
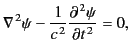
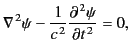

![]() ,
which yields
,
which yields
![]() , the small tangential component of
, the small tangential component of ![]() at
the walls can be estimated using Equation (1306):
at
the walls can be estimated using Equation (1306):