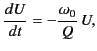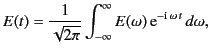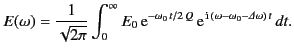Next: Axially Symmetric Cavities
Up: Resonant Cavities and Waveguides
Previous: Cavities with Rectangular Boundaries
The quality factor 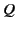 of a resonant cavity is defined
of a resonant cavity is defined
 |
(1320) |
For a specific normal mode of the cavity, this quantity is independent of
the mode amplitude. By conservation of energy, the power dissipated via
ohmic losses is minus the rate of change of the stored energy, 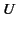 .
We can thus write a differential equation for the variation of
.
We can thus write a differential equation for the variation of 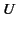 as
a function of time:
as
a function of time:
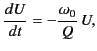 |
(1321) |
where 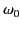 is the oscillation frequency of the normal mode in question.
The solution to the above equation is
is the oscillation frequency of the normal mode in question.
The solution to the above equation is
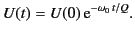 |
(1322) |
This time dependence of the stored energy suggests that the oscillations
of the electromagnetic fields inside the cavity are damped as follows:
 |
(1323) |
where we have allowed for a shift
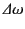 of the resonant frequency,
as well as for the damping.
A damped oscillation such as that specified above does not consist of a pure frequency.
Instead, it is made up of a superposition of frequencies centered on
of the resonant frequency,
as well as for the damping.
A damped oscillation such as that specified above does not consist of a pure frequency.
Instead, it is made up of a superposition of frequencies centered on
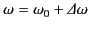 . Standard Fourier
analysis yields
. Standard Fourier
analysis yields
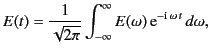 |
(1324) |
where
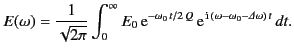 |
(1325) |
It follows that
 |
(1326) |
The above resonance curve has a full width at half-maximum equal to
 . For a constant input voltage, the energy of oscillation within
the cavity as a function of frequency follows this curve
in the neighborhood of a particular resonant frequency. It can be seen that
the ohmic losses, which determine
. For a constant input voltage, the energy of oscillation within
the cavity as a function of frequency follows this curve
in the neighborhood of a particular resonant frequency. It can be seen that
the ohmic losses, which determine 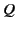 for a particular mode, also determine
the maximum amplitude of the oscillation when the resonance condition
is exactly satisfied, as well as the width of the resonance (i.e.,
how far off the resonant frequency the system can be driven, and still
yield a significant oscillation amplitude).
for a particular mode, also determine
the maximum amplitude of the oscillation when the resonance condition
is exactly satisfied, as well as the width of the resonance (i.e.,
how far off the resonant frequency the system can be driven, and still
yield a significant oscillation amplitude).



Next: Axially Symmetric Cavities
Up: Resonant Cavities and Waveguides
Previous: Cavities with Rectangular Boundaries
Richard Fitzpatrick
2014-06-27