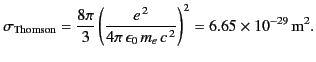Next: Rayleigh Scattering
Up: Radiation and Scattering
Previous: Antenna Arrays
When an electromagnetic wave is incident on a charged particle, the
electric and magnetic components of the wave exert a Lorentz force
on the particle, setting it into motion. Because the wave is periodic
in time, so is the motion of the particle. Thus, the particle is accelerated
and, consequently, emits radiation. More exactly, energy is
absorbed from the incident wave by the particle,
and re-emitted as electromagnetic radiation. Such
a process is clearly equivalent to the scattering of the electromagnetic
wave by the particle.
Consider a linearly polarized, monochromatic, plane wave incident on a
particle of charge 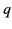 . The electric component of the wave can be
written
. The electric component of the wave can be
written
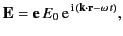 |
(1273) |
where 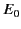 is the peak amplitude of the electric field,
is the peak amplitude of the electric field, 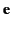 is
the polarization vector, and
is
the polarization vector, and 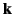 is the wave vector
(of course,
is the wave vector
(of course,
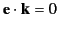 ).
The particle is assumed to undergo small
amplitude oscillations about an equilibrium position that coincides with
the origin of the coordinate system. Furthermore,
the particle's velocity is assumed
to remain sub-relativistic, which enables us to neglect the magnetic
component of the Lorentz force. The equation of motion of
the charged particle is approximately
).
The particle is assumed to undergo small
amplitude oscillations about an equilibrium position that coincides with
the origin of the coordinate system. Furthermore,
the particle's velocity is assumed
to remain sub-relativistic, which enables us to neglect the magnetic
component of the Lorentz force. The equation of motion of
the charged particle is approximately
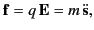 |
(1274) |
where 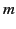 is the mass of the particle,
is the mass of the particle, 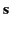 is its displacement from the origin, and
is its displacement from the origin, and 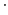 denotes
denotes
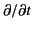 .
By analogy with Equation (1234), the time-averaged power radiated per unit solid
angle by an accelerating, non-relativistic, charged particle is given by
.
By analogy with Equation (1234), the time-averaged power radiated per unit solid
angle by an accelerating, non-relativistic, charged particle is given by
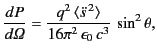 |
(1275) |
where
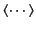 denotes a time average. Here, we are effectively treating the oscillating particle as a
short antenna.
However,
denotes a time average. Here, we are effectively treating the oscillating particle as a
short antenna.
However,
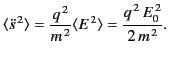 |
(1276) |
Hence, the scattered power per unit solid angle becomes
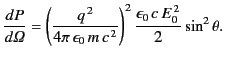 |
(1277) |
The time-averaged Poynting flux of the incident wave is
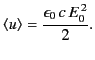 |
(1278) |
It is convenient to define the scattering cross-section as the equivalent area of the incident wavefront that delivers the same power as that
re-radiated
by the particle: that is,
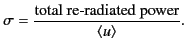 |
(1279) |
By analogy, the differential scattering cross-section is
defined
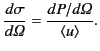 |
(1280) |
It follows from Equations (1279) and (1280) that
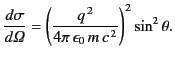 |
(1281) |
The total scattering cross-section is then
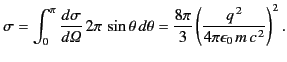 |
(1282) |
The quantity 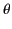 , appearing in Equation (1283), is the angle
subtended between the direction
of acceleration of the particle, and the direction of the outgoing radiation
(which is parallel to the unit vector
, appearing in Equation (1283), is the angle
subtended between the direction
of acceleration of the particle, and the direction of the outgoing radiation
(which is parallel to the unit vector 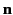 ). In the present case,
the acceleration is due to the electric field, so it is parallel to the
polarization vector
). In the present case,
the acceleration is due to the electric field, so it is parallel to the
polarization vector 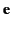 . Thus,
. Thus,
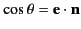 .
.
Up to now, we have only considered the scattering of linearly polarized
radiation by a charged particle. Let us now calculate the
angular distribution of scattered radiation for the commonly
occurring case of randomly polarized incident radiation. It is helpful
to set up a right-handed coordinate system based on the three
mutually orthogonal unit vectors 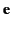 ,
,
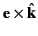 ,
and
,
and
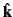 , where
, where
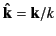 . In terms of these unit vectors, we can write
. In terms of these unit vectors, we can write
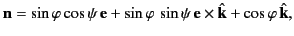 |
(1283) |
where 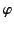 is the angle subtended between the direction of
the incident radiation and that of
the scattered radiation, and
is the angle subtended between the direction of
the incident radiation and that of
the scattered radiation, and 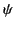 is an angle that
specifies the orientation of the polarization vector in the plane
perpendicular to
is an angle that
specifies the orientation of the polarization vector in the plane
perpendicular to 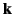 (assuming that
(assuming that 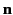 is known).
It is easily seen that
is known).
It is easily seen that
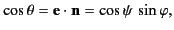 |
(1284) |
so
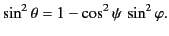 |
(1285) |
Averaging this result over all possible polarizations of the
incident wave (i.e., over all possible values of
the polarization angle 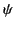 ), we obtain
), we obtain
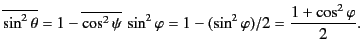 |
(1286) |
Thus, the differential scattering cross-section for unpolarized incident
radiation [obtained by substituting
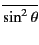 for
for
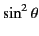 in Eq. (1283)] is given by
in Eq. (1283)] is given by
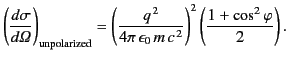 |
(1287) |
It is clear that the differential scattering cross-section is
independent of the frequency of the incident wave, and is also symmetric
with respect to forward and backward scattering. Moreover, the frequency of
the scattered radiation is the same as that of the incident radiation.
The total scattering cross-section is obtained by integrating over the entire
solid angle of the polar angle 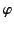 and the azimuthal
angle
and the azimuthal
angle 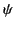 . Not surprisingly, the result
is exactly the same as Equation (1284).
. Not surprisingly, the result
is exactly the same as Equation (1284).
The classical scattering cross-section (1289) is modified by quantum
effects when the energy of the incident photons,
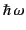 , becomes
comparable with the rest mass of the scattering particle,
, becomes
comparable with the rest mass of the scattering particle,
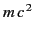 . The
scattering of a photon by a charged particle is called Compton
scattering, and the quantum mechanical version of the Compton scattering
cross-section is known as the Klein-Nishina cross-section. As the photon
energy increases, and eventually becomes comparable with the rest mass energy
of the particle, the Klein-Nishina formula predicts that forward scattering
of photons becomes increasingly favored with respect to backward scattering.
The Klein-Nishina cross-section does, in general, depend on the
frequency of the incident photons.
Furthermore, energy and momentum conservation demand a shift in the
frequency of scattered photons with respect to that of the incident photons.
. The
scattering of a photon by a charged particle is called Compton
scattering, and the quantum mechanical version of the Compton scattering
cross-section is known as the Klein-Nishina cross-section. As the photon
energy increases, and eventually becomes comparable with the rest mass energy
of the particle, the Klein-Nishina formula predicts that forward scattering
of photons becomes increasingly favored with respect to backward scattering.
The Klein-Nishina cross-section does, in general, depend on the
frequency of the incident photons.
Furthermore, energy and momentum conservation demand a shift in the
frequency of scattered photons with respect to that of the incident photons.
If the charged particle in question is an electron then Equation (1284)
reduces to the well-known Thomson scattering cross-section
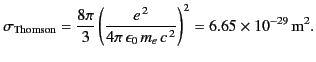 |
(1288) |
The quantity
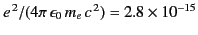 m is
called the classical electron radius (it is the radius of spherical
shell of total charge
m is
called the classical electron radius (it is the radius of spherical
shell of total charge 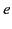 whose electrostatic energy equals the rest mass
energy of the electron). Thus, when scattering radiation, the electron acts rather like
a solid sphere whose radius is of order the classical electron
radius.
whose electrostatic energy equals the rest mass
energy of the electron). Thus, when scattering radiation, the electron acts rather like
a solid sphere whose radius is of order the classical electron
radius.



Next: Rayleigh Scattering
Up: Radiation and Scattering
Previous: Antenna Arrays
Richard Fitzpatrick
2014-06-27
![]() . The electric component of the wave can be
written
. The electric component of the wave can be
written
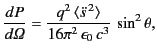
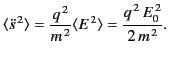
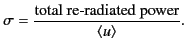
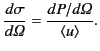
![]() ,
,
![]() ,
and
,
and
![]() , where
, where
![]() . In terms of these unit vectors, we can write
. In terms of these unit vectors, we can write
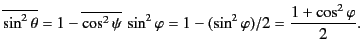
![]() , becomes
comparable with the rest mass of the scattering particle,
, becomes
comparable with the rest mass of the scattering particle,
![]() . The
scattering of a photon by a charged particle is called Compton
scattering, and the quantum mechanical version of the Compton scattering
cross-section is known as the Klein-Nishina cross-section. As the photon
energy increases, and eventually becomes comparable with the rest mass energy
of the particle, the Klein-Nishina formula predicts that forward scattering
of photons becomes increasingly favored with respect to backward scattering.
The Klein-Nishina cross-section does, in general, depend on the
frequency of the incident photons.
Furthermore, energy and momentum conservation demand a shift in the
frequency of scattered photons with respect to that of the incident photons.
. The
scattering of a photon by a charged particle is called Compton
scattering, and the quantum mechanical version of the Compton scattering
cross-section is known as the Klein-Nishina cross-section. As the photon
energy increases, and eventually becomes comparable with the rest mass energy
of the particle, the Klein-Nishina formula predicts that forward scattering
of photons becomes increasingly favored with respect to backward scattering.
The Klein-Nishina cross-section does, in general, depend on the
frequency of the incident photons.
Furthermore, energy and momentum conservation demand a shift in the
frequency of scattered photons with respect to that of the incident photons.