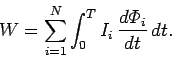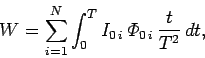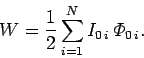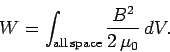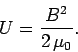Next: Alternating current circuits
Up: Magnetic induction
Previous: Mutual inductance
Suppose that at 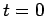 a coil of inductance,
a coil of inductance, 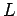 , and resistance,
, and resistance, 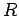 , is connected
across the terminals of a battery of e.m.f.,
, is connected
across the terminals of a battery of e.m.f.,  . The circuit equation is
. The circuit equation is
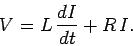 |
(932) |
The power output of the battery is 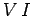 . [Every charge
. [Every charge 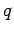 that goes around the circuit
falls through a potential difference
that goes around the circuit
falls through a potential difference 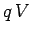 . In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work
. In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work 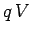 . The work done per unit time (i.e., the power) is
. The work done per unit time (i.e., the power) is 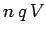 , where
, where 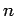 is
the number of charges per unit time passing a given point on the circuit.
But,
is
the number of charges per unit time passing a given point on the circuit.
But, 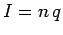 , so the power output is
, so the power output is 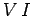 .] The total work done by the battery in
raising the current in the circuit from zero at time
.] The total work done by the battery in
raising the current in the circuit from zero at time 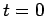 to
to 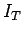 at
time
at
time 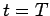 is
is
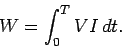 |
(933) |
Using the circuit equation (932), we obtain
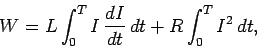 |
(934) |
giving
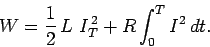 |
(935) |
The second term on the right-hand side represents the irreversible conversion of
electrical energy into heat energy in the resistor. The first term is the amount of
energy stored in the inductor at time 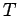 . This energy can be recovered after the
inductor is disconnected from the battery. Suppose that the battery is disconnected
at time
. This energy can be recovered after the
inductor is disconnected from the battery. Suppose that the battery is disconnected
at time 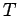 . The circuit equation is now
. The circuit equation is now
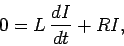 |
(936) |
giving
![\begin{displaymath}
I= I_T \exp \left[ - \frac{R}{L} (t-T) \right],
\end{displaymath}](img1952.png) |
(937) |
where we have made use of the boundary condition 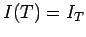 .
Thus, the current
decays away exponentially. The energy stored in the inductor is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
.
Thus, the current
decays away exponentially. The energy stored in the inductor is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
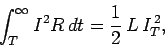 |
(938) |
where use has been made of Eq. (937).
Thus, the heat energy appearing in the resistor is equal to the
energy stored in the inductor. This energy is actually stored in the magnetic
field generated around the inductor.
Consider, again, our circuit with two coils wound on top of one another. Suppose that
each coil is connected to its own battery. The circuit equations are thus
where 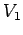 is the e.m.f. of the battery in the first circuit, etc.
The work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to
is the e.m.f. of the battery in the first circuit, etc.
The work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to 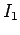 and
and 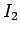 at time
at time 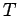 , respectively, is
, respectively, is
Thus,
Clearly, the total magnetic energy stored in the two coils is
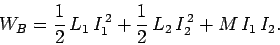 |
(942) |
Note that the mutual inductance term increases the stored magnetic energy if 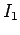 and
and
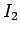 are of the same sign--i.e., if the currents in the two coils flow
in the same direction, so that they generate magnetic fields which reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if
are of the same sign--i.e., if the currents in the two coils flow
in the same direction, so that they generate magnetic fields which reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if 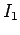 and
and 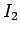 are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
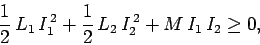 |
(943) |
which can be written
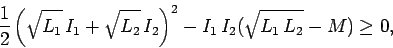 |
(944) |
assuming that  . It follows that
. It follows that
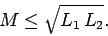 |
(945) |
The equality sign corresponds to the situation where
all of the flux generated by one coil passes through the other. If some of
the flux misses then the inequality sign is appropriate.
In fact, the above formula is valid
for any two inductively coupled circuits.
We intimated previously that the energy stored in an inductor is actually
stored in the surrounding magnetic field. Let us now obtain an
explicit formula for the energy stored in a magnetic field. Consider an ideal
solenoid. The energy stored in the solenoid when a current 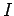 flows through it
is
flows through it
is
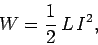 |
(946) |
where 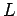 is the self-inductance. We know that
is the self-inductance. We know that
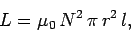 |
(947) |
where  is the number of turns per unit length of the
solenoid,
is the number of turns per unit length of the
solenoid, 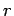 the radius, and
the radius, and 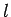 the length. The field inside the solenoid is
uniform, with magnitude
the length. The field inside the solenoid is
uniform, with magnitude
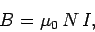 |
(948) |
and is zero outside the solenoid. Equation (946) can be rewritten
 |
(949) |
where
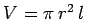 is the volume of the solenoid. The above formula strongly
suggests that a magnetic field possesses an energy density
is the volume of the solenoid. The above formula strongly
suggests that a magnetic field possesses an energy density
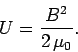 |
(950) |
Let us now examine a more general proof of the above formula. Consider a system
of  circuits (labeled
circuits (labeled 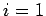 to
to  ), each carrying a current
), each carrying a current 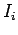 .
The magnetic flux through the
.
The magnetic flux through the 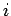 th circuit is written [cf., Eq. (900)]
th circuit is written [cf., Eq. (900)]
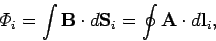 |
(951) |
where
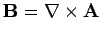 , and
, and 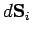 and
and 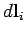 denote a
surface element and a line element of this circuit, respectively. The
back e.m.f. induced in the
denote a
surface element and a line element of this circuit, respectively. The
back e.m.f. induced in the 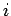 th circuit follows from Faraday's law:
th circuit follows from Faraday's law:
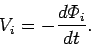 |
(952) |
The rate of work of the battery which maintains the current 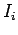 in the
in the 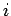 th circuit
against this back e.m.f. is
th circuit
against this back e.m.f. is
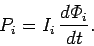 |
(953) |
Thus, the total work required
to raise the currents in the  circuits from zero at time
0, to
circuits from zero at time
0, to 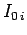 at time
at time 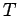 , is
, is
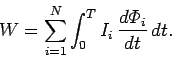 |
(954) |
The above expression for the work done is, of course, equivalent to the total
energy stored in the magnetic field surrounding the various circuits.
This energy is independent of the manner in which the currents
are set up.
Suppose, for the sake of simplicity, that the currents are ramped up linearly,
so that
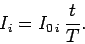 |
(955) |
The fluxes are proportional to the currents, so they must also ramp up linearly:
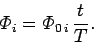 |
(956) |
It follows that
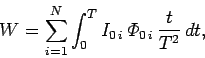 |
(957) |
giving
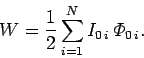 |
(958) |
So, if instantaneous currents 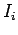 flow in the the
flow in the the  circuits, which link
instantaneous fluxes
circuits, which link
instantaneous fluxes 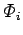 , then the instantaneous stored energy is
, then the instantaneous stored energy is
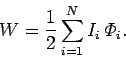 |
(959) |
Equations (951) and (959) imply that
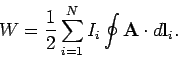 |
(960) |
It is convenient, at this stage, to replace our  line currents by
line currents by
 current
distributions of
small, but finite, cross-sectional area.
Equation (960)
transforms to
current
distributions of
small, but finite, cross-sectional area.
Equation (960)
transforms to
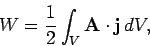 |
(961) |
where  is a volume which contains all of the circuits.
Note that for an element of the
is a volume which contains all of the circuits.
Note that for an element of the 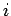 th circuit
th circuit
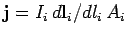 and
and
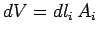 , where
, where 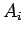 is the cross-sectional area of the
circuit.
Now,
is the cross-sectional area of the
circuit.
Now,
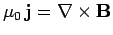 (we are neglecting the displacement
current in this calculation), so
(we are neglecting the displacement
current in this calculation), so
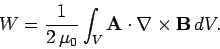 |
(962) |
According to vector field theory,
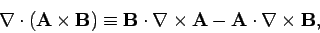 |
(963) |
which implies that
![\begin{displaymath}
W = \frac{1}{2 \mu_0} \int_V \left[- \nabla\cdot ({\bf A} \times{\bf B})
+{\bf B}\cdot \nabla \times {\bf A} \right] dV.
\end{displaymath}](img1998.png) |
(964) |
Using Gauss' theorem, and
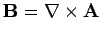 , we obtain
, we obtain
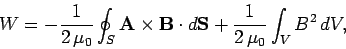 |
(965) |
where  is the bounding surface of
is the bounding surface of  . Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like
. Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like  at large distances. The vector potential
falls off like
at large distances. The vector potential
falls off like 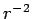 . However, the area of surface
. However, the area of surface  only increases like
only increases like 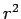 .
It follows that the surface integral is negligible in the limit
.
It follows that the surface integral is negligible in the limit
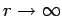 .
Thus, the above expression reduces to
.
Thus, the above expression reduces to
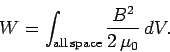 |
(966) |
Since this expression is valid for any magnetic field whatsoever, we can safely conclude
that the energy density of a general magnetic field is given by
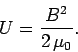 |
(967) |
Note, also, that the above expression is consistent with the expression
(894) which we obtained during our investigation of magnetic
media.



Next: Alternating current circuits
Up: Magnetic induction
Previous: Mutual inductance
Richard Fitzpatrick
2006-02-02
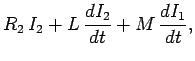
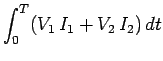
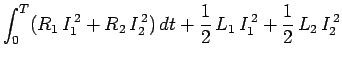
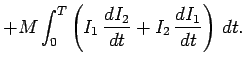
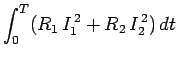
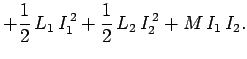
![]() flows through it
is
flows through it
is

![]() circuits (labeled
circuits (labeled ![]() to
to ![]() ), each carrying a current
), each carrying a current ![]() .
The magnetic flux through the
.
The magnetic flux through the ![]() th circuit is written [cf., Eq. (900)]
th circuit is written [cf., Eq. (900)]