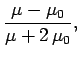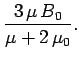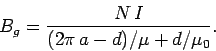Next: Magnetic energy
Up: Dielectric and magnetic media
Previous: Boundary conditions for and
Consider a ferromagnetic sphere, of uniform permeability 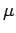 , placed in
a uniform
, placed in
a uniform  -directed magnetic field of magnitude
-directed magnetic field of magnitude 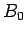 . Suppose
that the sphere is centred on the origin. In the absence of any true currents,
we have
. Suppose
that the sphere is centred on the origin. In the absence of any true currents,
we have
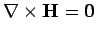 . Hence, we can write
. Hence, we can write
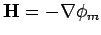 . Given that
. Given that
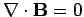 , and
, and
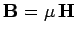 , it follows that
, it follows that
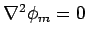 in any uniform magnetic medium
(or a vacuum). Hence,
in any uniform magnetic medium
(or a vacuum). Hence,
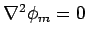 throughout space. Adopting spherical polar coordinates,
throughout space. Adopting spherical polar coordinates,
 , aligned along the
, aligned along the  -axis, the boundary
conditions are that
-axis, the boundary
conditions are that
 at
at
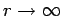 , and that
, and that  is well-behaved at
is well-behaved at 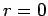 . At the surface of the sphere,
. At the surface of the sphere, 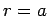 , the continuity of
, the continuity of 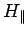 implies that
implies that  is continuous. Furthermore, the
continuity of
is continuous. Furthermore, the
continuity of
 leads to the matching condition
leads to the matching condition
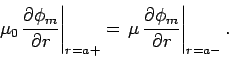 |
(875) |
Let us try separable solutions of the form
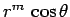 . It is
easily demonstrated that such solutions satisfy Laplace's equation
provided that
. It is
easily demonstrated that such solutions satisfy Laplace's equation
provided that 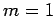 or
or  . Hence, the most general solution to Laplace's equation outside
the sphere, which satisfies the boundary condition at
. Hence, the most general solution to Laplace's equation outside
the sphere, which satisfies the boundary condition at
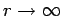 , is
, is
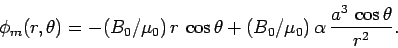 |
(876) |
Likewise, the most general solution inside the sphere, which satisfies
the boundary condition at 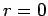 , is
, is
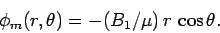 |
(877) |
The continuity of  at
at 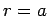 yields
yields
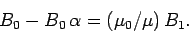 |
(878) |
Likewise, the matching condition (875) gives
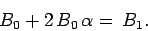 |
(879) |
Hence,
Note that the magnetic field inside the sphere is uniform, parallel
to the external magnetic field outside the sphere, and of magnitude 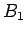 . Moreover,
. Moreover,  , provided that
, provided that 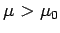 .
.
Figure 50:
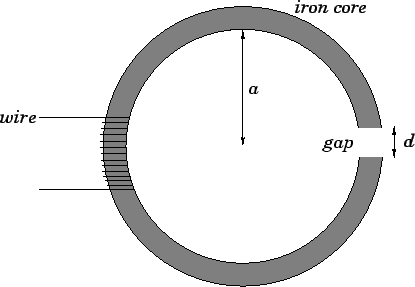 |
As a final example, consider an electromagnet of the form sketched in Fig. 50. A wire, carrying a current 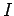 , is wrapped
, is wrapped 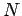 times
around a thin toroidal iron core of radius
times
around a thin toroidal iron core of radius  and permeability
and permeability 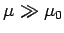 . The core contains
a thin gap of width
. The core contains
a thin gap of width 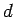 . What is the magnetic field induced in the
gap?
Let us neglect any leakage of magnetic field from the core, which is
reasonable if
. What is the magnetic field induced in the
gap?
Let us neglect any leakage of magnetic field from the core, which is
reasonable if 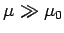 . We expect the magnetic field,
. We expect the magnetic field,  ,
and the magnetic intensity,
,
and the magnetic intensity, 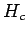 , in the core to be both toroidal and essentially
uniform. It is also reasonable to suppose that the magnetic field,
, in the core to be both toroidal and essentially
uniform. It is also reasonable to suppose that the magnetic field, 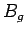 , and the
magnetic intensity,
, and the
magnetic intensity,  , in the gap are toroidal and uniform, since
, in the gap are toroidal and uniform, since
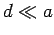 . We have
. We have
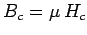 and
and
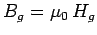 .
Moreover, since the magnetic field is normal to the interface between the
core and the gap, the continuity of
.
Moreover, since the magnetic field is normal to the interface between the
core and the gap, the continuity of 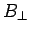 implies that
implies that
 |
(882) |
Thus, the magnetic field-strength in the core is the same as that in the
gap. However, the magnetic intensities in the core and the gap are
quite different:
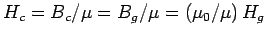 .
Integration of Eq. (871) around the torus yields
.
Integration of Eq. (871) around the torus yields
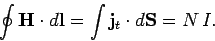 |
(883) |
Hence,
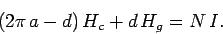 |
(884) |
It follows that
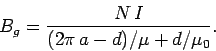 |
(885) |



Next: Magnetic energy
Up: Dielectric and magnetic media
Previous: Boundary conditions for and
Richard Fitzpatrick
2006-02-02
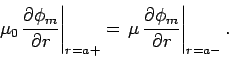
![]() . It is
easily demonstrated that such solutions satisfy Laplace's equation
provided that
. It is
easily demonstrated that such solutions satisfy Laplace's equation
provided that ![]() or
or ![]() . Hence, the most general solution to Laplace's equation outside
the sphere, which satisfies the boundary condition at
. Hence, the most general solution to Laplace's equation outside
the sphere, which satisfies the boundary condition at
![]() , is
, is