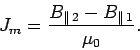Next: Boundary value problems with
Up: Dielectric and magnetic media
Previous: Ferromagnetism
What are the boundary conditions for 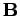 and
and  at
the interface between two magnetic media? The governing equations for a steady-state situation are
at
the interface between two magnetic media? The governing equations for a steady-state situation are
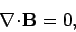 |
(870) |
and
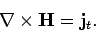 |
(871) |
Integrating Eq. (870) over a Gaussian pill-box enclosing part of the
interface between the two media gives
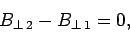 |
(872) |
where 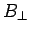 denotes the component of
denotes the component of 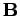 perpendicular to
the interface.
Integrating Eq. (871) around a small loop which
straddles the interface yields
perpendicular to
the interface.
Integrating Eq. (871) around a small loop which
straddles the interface yields
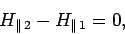 |
(873) |
assuming that there is no true current sheet flowing in the interface.
Here, 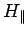 denotes the component of
denotes the component of  parallel to the
interface.
In general, there is a magnetization current sheet flowing
at the interface whose density is of amplitude
parallel to the
interface.
In general, there is a magnetization current sheet flowing
at the interface whose density is of amplitude
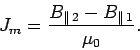 |
(874) |
In conclusion, the normal component of the magnetic field
and the tangential component of the magnetic intensity are both
continuous across any interface between magnetic media.



Next: Boundary value problems with
Up: Dielectric and magnetic media
Previous: Ferromagnetism
Richard Fitzpatrick
2006-02-02