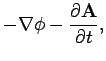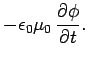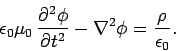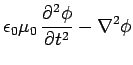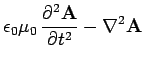Next: Electromagnetic waves
Up: Time-dependent Maxwell's equations
Previous: The displacement current
Potential formulation
We have seen that Eqs. (418) and (419) are automatically satisfied
if we write the electric and magnetic fields in terms of potentials:
This prescription is not unique, but we can make it unique by adopting the
following conventions:
The above equations can be combined with Eq. (417) to give
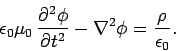 |
(425) |
Let us now consider Eq. (420). Substitution of Eqs. (421) and (422) into this formula
yields
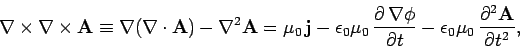 |
(426) |
or
 |
(427) |
We can now see quite clearly
where the Lorentz gauge condition (398) comes from. The above
equation is, in general, very complicated, since it involves both the vector and
scalar potentials. But, if we adopt the Lorentz gauge, then the last term on
the right-hand side becomes zero, and the equation simplifies considerably, such that
it only involves the vector potential. Thus, we find that Maxwell's equations
reduce to the following:
This is the same (scalar) equation written four times over. In steady-state (i.e.,
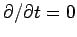 ), it reduces to Poisson's equation, which we know
how to solve. With the
), it reduces to Poisson's equation, which we know
how to solve. With the
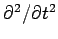 terms included,
it becomes a slightly more complicated equation (in fact, a
driven three-dimensional wave equation).
terms included,
it becomes a slightly more complicated equation (in fact, a
driven three-dimensional wave equation).



Next: Electromagnetic waves
Up: Time-dependent Maxwell's equations
Previous: The displacement current
Richard Fitzpatrick
2006-02-02