| (400) | |||
| (401) | |||
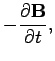 |
(402) | ||
| (403) |
We can see that there is something slightly unusual about
Eqs. (400)-(403). They
are very unfair to electric fields! After all, time-varying magnetic fields
can induce electric fields, but electric fields apparently
cannot affect magnetic fields
in any way. However, there is a far more serious problem associated
with the above equations,
which we alluded to earlier on. Consider the integral form of the last
Maxwell equation
(i.e., Ampère's circuital law)
| (405) |
Why do we say that, in general,
![]() ? Well, consider
the flux of
? Well, consider
the flux of ![]() out of some closed surface
out of some closed surface ![]() enclosing a
volume
enclosing a
volume ![]() . This is clearly equivalent to the rate at which
charge flows out of
. This is clearly equivalent to the rate at which
charge flows out of ![]() . However, if charge is a conserved quantity
(and we certainly
believe that it is) then the rate at which charge flows out of
. However, if charge is a conserved quantity
(and we certainly
believe that it is) then the rate at which charge flows out of ![]() must
equal
the rate of decrease of the charge contained in volume
must
equal
the rate of decrease of the charge contained in volume ![]() . Thus,
. Thus,
| (406) |
The problem with Ampère's circuital law is well illustrated by the following very famous
example.
Consider a long straight wire interrupted by a parallel plate capacitor. Suppose
that ![]() is some loop which circles the wire. In the non time-dependent situation, the
capacitor acts like a break in the wire, so no current flows, and no magnetic
field is generated. There is clearly no problem with Ampère's law in this case.
However, in the time-dependent situation, a transient current flows in the wire as the
capacitor charges up, or charges down, and so a transient magnetic field is generated.
Thus, the line integral of the magnetic field around
is some loop which circles the wire. In the non time-dependent situation, the
capacitor acts like a break in the wire, so no current flows, and no magnetic
field is generated. There is clearly no problem with Ampère's law in this case.
However, in the time-dependent situation, a transient current flows in the wire as the
capacitor charges up, or charges down, and so a transient magnetic field is generated.
Thus, the line integral of the magnetic field around ![]() is
(transiently) non-zero. According to Ampère's circuital law, the flux of the current
through any surface attached to
is
(transiently) non-zero. According to Ampère's circuital law, the flux of the current
through any surface attached to ![]() should also be (transiently) non-zero.
Let us consider two such surfaces. The
first surface,
should also be (transiently) non-zero.
Let us consider two such surfaces. The
first surface, ![]() , intersects the wire. This surface
causes us no problem, since the flux of
, intersects the wire. This surface
causes us no problem, since the flux of ![]() though the surface is clearly
non-zero (because it intersects
a current carrying wire).
The second surface,
though the surface is clearly
non-zero (because it intersects
a current carrying wire).
The second surface, ![]() , passes between the plates of the capacitor, and, therefore,
does not intersect the wire at all. Clearly, the flux of the current through
this surface is zero. The current fluxes through surfaces
, passes between the plates of the capacitor, and, therefore,
does not intersect the wire at all. Clearly, the flux of the current through
this surface is zero. The current fluxes through surfaces ![]() and
and ![]() are obviously different. However, both surfaces are attached to the same loop
are obviously different. However, both surfaces are attached to the same loop ![]() ,
so
the fluxes should be the same, according to Ampère's law (404). It would appear
that Ampère's circuital law is about to disintegrate! However,
we notice that although the surface
,
so
the fluxes should be the same, according to Ampère's law (404). It would appear
that Ampère's circuital law is about to disintegrate! However,
we notice that although the surface ![]() does not intersect any electric current,
it does pass through a region of strong changing
electric field as it threads between the
plates of the charging (or discharging) capacitor. Perhaps, if we add a term involving
does not intersect any electric current,
it does pass through a region of strong changing
electric field as it threads between the
plates of the charging (or discharging) capacitor. Perhaps, if we add a term involving
![]() to the right-hand side of Eq. (403) then we
can somehow fix up Ampère's circuital law? This is, essentially, how Maxwell reasoned
more than one hundred years ago.
to the right-hand side of Eq. (403) then we
can somehow fix up Ampère's circuital law? This is, essentially, how Maxwell reasoned
more than one hundred years ago.
Let us try out this scheme. Suppose that we write
| (409) |
| (410) |
| (411) |
| (412) |
Of course, the displacement current is not a current at all. It is, in fact, associated with the generation of magnetic fields by time-varying electric fields. Maxwell came up with this rather curious name because many of his ideas regarding electric and magnetic fields were completely wrong. For instance, Maxwell believed in the æther, and he thought that electric and magnetic fields were some sort of stresses in this medium. He also thought that the displacement current was associated with displacements of the æther (hence, the name). The reason that these misconceptions did not invalidate his equations is quite simple. Maxwell based his equations on the results of experiments, and he added in his extra term so as to make these equations mathematically self-consistent. Both of these steps are valid irrespective of the existence or non-existence of the æther.
``But, hang on a minute,'' you might say, ``you can't go around adding terms to laws of physics just because you feel like it! The field equations (400)-(403) are derived directly from the results of famous nineteenth century experiments. If there is a new term involving the time derivative of the electric field which needs to be added into these equations, how come there is no corresponding nineteenth century experiment which demonstrates this? We have Faraday's law which shows that changing magnetic fields generate electric fields. Why is there no ``Joe Blogg's'' law that says that changing electric fields generate magnetic fields?'' This is a perfectly reasonable question. The answer is that the new term describes an effect which is far too small to have been observed in nineteenth century experiments. Let us demonstrate this.
First, we shall show that it is comparatively easy to detect the induction of
an electric field by a changing magnetic field in a desktop laboratory experiment.
The Earth's magnetic field is about 1 gauss (that is, ![]() tesla).
Magnetic fields generated by electromagnets (which will fit on a laboratory desktop)
are typically about one hundred times bigger that this. Let us, therefore,
consider a hypothetical experiment in which a 100 gauss magnetic field is
switched on suddenly. Suppose that the field ramps up in one tenth of a second.
What electromotive force is generated in a 10 centimeter square loop of wire
located in this field? Faraday's law is written
tesla).
Magnetic fields generated by electromagnets (which will fit on a laboratory desktop)
are typically about one hundred times bigger that this. Let us, therefore,
consider a hypothetical experiment in which a 100 gauss magnetic field is
switched on suddenly. Suppose that the field ramps up in one tenth of a second.
What electromotive force is generated in a 10 centimeter square loop of wire
located in this field? Faraday's law is written
| (414) |
Let us now consider the electric induction of magnetic fields. Suppose that our
electric field is generated by a parallel plate capacitor of spacing one centimeter
which is charged up
to ![]() volts. This gives a field of
volts. This gives a field of ![]() volts per meter. Suppose,
further, that the capacitor is discharged in one tenth of a second. The law
of electric induction is obtained by integrating Eq. (413), and neglecting the
first term on the right-hand side. Thus,
volts per meter. Suppose,
further, that the capacitor is discharged in one tenth of a second. The law
of electric induction is obtained by integrating Eq. (413), and neglecting the
first term on the right-hand side. Thus,
| (415) |
| (416) |
``So,'' you might say, ``why did you bother mentioning this displacement current
thing in the first place if it is undetectable?'' Again, a perfectly fair question.
The answer is that the displacement current is detectable in some experiments.
Suppose that we take an FM radio signal, amplify it so that its peak
voltage is one hundred volts, and then apply it to
the parallel plate capacitor in the previous hypothetical experiment.
What size of magnetic
field would this generate? Well, a typical FM signal oscillates at ![]() Hz,
so
Hz,
so ![]() in the previous example changes from
in the previous example changes from ![]() seconds to
seconds to ![]() seconds.
Thus, the induced magnetic field is about
seconds.
Thus, the induced magnetic field is about ![]() gauss. This
is certainly detectable by modern technology. So, it would
seem that if the electric field is oscillating fast then electric induction
of magnetic fields is an observable effect. In fact, there is a virtually
infallible rule for deciding whether or not the displacement current can be
neglected in Eq. (413). If electromagnetic radiation is important
then the displacement current must be included. On the other hand, if
electromagnetic radiation is unimportant then the displacement current can be
safely neglected. Clearly, Maxwell's inclusion of the displacement current in
Eq. (413) was a vital step in his later realization that his equations allowed
propagating wave-like solutions. These solutions
are, of course, electromagnetic waves.
But, more of this later.
gauss. This
is certainly detectable by modern technology. So, it would
seem that if the electric field is oscillating fast then electric induction
of magnetic fields is an observable effect. In fact, there is a virtually
infallible rule for deciding whether or not the displacement current can be
neglected in Eq. (413). If electromagnetic radiation is important
then the displacement current must be included. On the other hand, if
electromagnetic radiation is unimportant then the displacement current can be
safely neglected. Clearly, Maxwell's inclusion of the displacement current in
Eq. (413) was a vital step in his later realization that his equations allowed
propagating wave-like solutions. These solutions
are, of course, electromagnetic waves.
But, more of this later.
We are now in a position to write out Maxwell's equations in all their glory!
We get