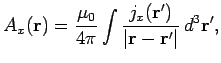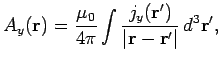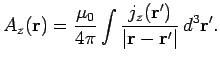Next: The Biot-Savart law
Up: Time-independent Maxwell equations
Previous: Helmholtz's theorem
The magnetic vector potential
Electric fields generated by stationary charges obey
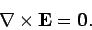 |
(315) |
This immediately allows us to write
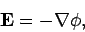 |
(316) |
since the curl of a gradient is automatically zero. In fact, whenever we come
across an irrotational vector field in physics we can always write it as the
gradient of some scalar field. This is clearly a useful thing to do, since it
enables us to
replace a vector field by a much simpler scalar field.
The quantity  in the above equation
is known as the electric scalar potential.
in the above equation
is known as the electric scalar potential.
Magnetic fields generated by steady currents (and unsteady currents, for that matter)
satisfy
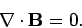 |
(317) |
This immediately allows us to write
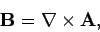 |
(318) |
since the divergence of a curl is automatically zero. In fact, whenever we come
across a solenoidal vector field in physics we can always write it as the curl
of some other
vector field. This is not an obviously useful thing to do, however, since
it only allows us to replace one vector field by another. Nevertheless, Eq. (318)
is one of the
most useful equations we shall come across in this lecture course. The quantity
 is known as the magnetic vector potential.
is known as the magnetic vector potential.
We know from Helmholtz's theorem that a vector field is fully specified by
its divergence and its curl. The curl of the vector potential gives us the magnetic
field via Eq. (318). However, the divergence of  has no physical
significance. In fact, we are completely free to choose
has no physical
significance. In fact, we are completely free to choose
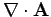 to
be whatever we like. Note that, according to Eq. (318), the magnetic field
is invariant under the transformation
to
be whatever we like. Note that, according to Eq. (318), the magnetic field
is invariant under the transformation
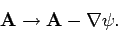 |
(319) |
In other words, the vector potential is undetermined to the gradient of a scalar
field. This is just another way of saying that we are free to choose
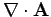 . Recall that the electric scalar potential is undetermined to an
arbitrary additive constant, since the transformation
. Recall that the electric scalar potential is undetermined to an
arbitrary additive constant, since the transformation
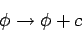 |
(320) |
leaves the electric field invariant in Eq. (316). The transformations (319)
and (320) are examples of what mathematicians call gauge transformations.
The choice of a particular function 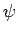 or a particular constant
or a particular constant 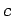 is
referred to as a choice of the
gauge. We are free to fix the gauge to be whatever we
like. The most sensible choice is the one which makes our equations as simple
as possible. The usual gauge for the scalar potential
is
referred to as a choice of the
gauge. We are free to fix the gauge to be whatever we
like. The most sensible choice is the one which makes our equations as simple
as possible. The usual gauge for the scalar potential  is such
that
is such
that
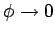 at infinity. The usual gauge for
at infinity. The usual gauge for  is such that
is such that
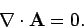 |
(321) |
This particular choice is known as the Coulomb gauge.
It is obvious that we can always add a constant to  so as to make
it zero at infinity. But it is not at all obvious that we can always
perform a gauge transformation such as to make
so as to make
it zero at infinity. But it is not at all obvious that we can always
perform a gauge transformation such as to make
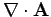 zero.
Suppose that we have found some vector field
zero.
Suppose that we have found some vector field  whose curl gives the
magnetic field but whose divergence in non-zero. Let
whose curl gives the
magnetic field but whose divergence in non-zero. Let
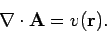 |
(322) |
The question is, can we find a scalar field 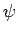 such that after we perform the
gauge transformation (319) we are left with
such that after we perform the
gauge transformation (319) we are left with
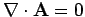 . Taking
the divergence of Eq. (319) it is clear that we need to find a
function
. Taking
the divergence of Eq. (319) it is clear that we need to find a
function 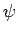 which
satisfies
which
satisfies
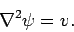 |
(323) |
But this is just Poisson's equation. We know that we can always find a
unique solution of this equation (see Sect. 3.11). This proves that, in practice,
we can always set the divergence of  equal to zero.
equal to zero.
Let us again consider an infinite straight wire directed along the  -axis and
carrying a current
-axis and
carrying a current 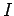 . The magnetic field generated by such a wire is
written
. The magnetic field generated by such a wire is
written
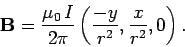 |
(324) |
We wish to find a vector potential  whose curl is equal to the above magnetic field, and whose divergence is
zero. It is not difficult to see that
whose curl is equal to the above magnetic field, and whose divergence is
zero. It is not difficult to see that
![\begin{displaymath}
{\bf A} = -\frac{\mu_0 I}{4\pi} \left( 0, 0, \ln[x^2+y^2] \right)
\end{displaymath}](img863.png) |
(325) |
fits the bill.
Note that the vector potential is parallel to the direction of the current. This
would seem to suggest that there is a more direct relationship between
the vector potential and the current than there is between the magnetic field
and the current. The potential is not very well-behaved on the  -axis, but this
is just because we are dealing with an infinitely thin current.
-axis, but this
is just because we are dealing with an infinitely thin current.
Let us take the curl of Eq. (318). We find that
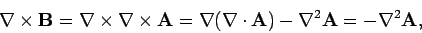 |
(326) |
where use has been made of the Coulomb gauge condition
(321). We can combine the above
relation with the field equation (274) to give
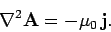 |
(327) |
Writing this in component form, we obtain
But, this is just Poisson's equation three times over. We can immediately
write the unique solutions to the above equations:
These solutions can be recombined to form a single vector solution
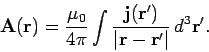 |
(334) |
Of course, we have seen a equation like this before:
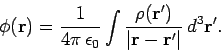 |
(335) |
Equations (334) and (335) are the unique solutions (given the arbitrary choice
of gauge) to the field equations (279)-(282): they specify the magnetic
vector and electric scalar potentials generated by a set of stationary
charges, of charge density 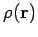 , and a set of steady currents,
of current density
, and a set of steady currents,
of current density
 . Incidentally, we can prove that
Eq. (334) satisfies the gauge condition
. Incidentally, we can prove that
Eq. (334) satisfies the gauge condition
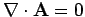 by repeating
the analysis of Eqs. (300)-(307) (with
by repeating
the analysis of Eqs. (300)-(307) (with
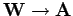 and
and
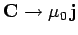 ), and using the fact that
), and using the fact that
 for steady currents.
for steady currents.



Next: The Biot-Savart law
Up: Time-independent Maxwell equations
Previous: Helmholtz's theorem
Richard Fitzpatrick
2006-02-02
![]() has no physical
significance. In fact, we are completely free to choose
has no physical
significance. In fact, we are completely free to choose
![]() to
be whatever we like. Note that, according to Eq. (318), the magnetic field
is invariant under the transformation
to
be whatever we like. Note that, according to Eq. (318), the magnetic field
is invariant under the transformation
![]() so as to make
it zero at infinity. But it is not at all obvious that we can always
perform a gauge transformation such as to make
so as to make
it zero at infinity. But it is not at all obvious that we can always
perform a gauge transformation such as to make
![]() zero.
Suppose that we have found some vector field
zero.
Suppose that we have found some vector field ![]() whose curl gives the
magnetic field but whose divergence in non-zero. Let
whose curl gives the
magnetic field but whose divergence in non-zero. Let
![]() -axis and
carrying a current
-axis and
carrying a current ![]() . The magnetic field generated by such a wire is
written
. The magnetic field generated by such a wire is
written