


Next: Electrostatics and magnetostatics
Up: Time-independent Maxwell equations
Previous: The magnetic vector potential
According to Eq. (316), we can obtain an expression for the electric field
generated by stationary charges by
taking minus the gradient of Eq. (335). This yields
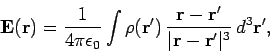 |
(336) |
which we recognize as Coulomb's law written for a continuous charge distribution.
According to Eq. (318), we can obtain an equivalent expression for the magnetic
field generated by steady currents by taking the curl of Eq. (334). This gives
 |
(337) |
where use has been made of the vector identity
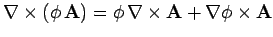 . Equation (337) is
known as the Biot-Savart law after the French physicists Jean Baptiste
Biot and Felix Savart: it completely specifies the magnetic field generated
by a steady (but otherwise quite general) distributed current.
. Equation (337) is
known as the Biot-Savart law after the French physicists Jean Baptiste
Biot and Felix Savart: it completely specifies the magnetic field generated
by a steady (but otherwise quite general) distributed current.
Let us reduce our distributed current to
an idealized zero thickness wire. We can do this by writing
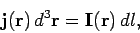 |
(338) |
where 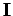 is the vector current (i.e., its direction and magnitude specify
the direction and magnitude of the current) and
is the vector current (i.e., its direction and magnitude specify
the direction and magnitude of the current) and
 is an element of length along the wire. Equations (337) and (338) can
be combined to give
is an element of length along the wire. Equations (337) and (338) can
be combined to give
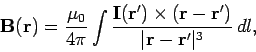 |
(339) |
which is the form in which the Biot-Savart law is most usually written.
This law is to magnetostatics (i.e., the study of magnetic
fields generated by steady currents) what Coulomb's law is to electrostatics
(i.e., the study of electric fields generated by stationary charges). Furthermore,
it can be experimentally verified given a set of currents, a
compass, a test wire, and a great deal of skill and patience. This
justifies our
earlier assumption that the field equations (277) and (278) are valid for general
current distributions (recall that we derived them by studying the fields
generated by infinite, straight wires). Note that both Coulomb's law and
the Biot-Savart law are gauge independent: i.e., they do not depend on the
particular choice of gauge.
Figure 33:
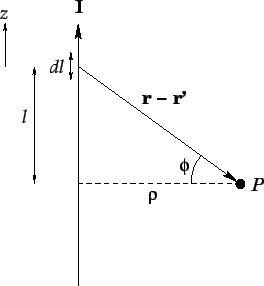 |
Consider an infinite straight wire, directed along the
 -axis, and carrying a current
-axis, and carrying a current 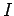 (see Fig. 33).
Let us reconstruct the magnetic field generated by the wire at point
(see Fig. 33).
Let us reconstruct the magnetic field generated by the wire at point
 using the Biot-Savart
law. Suppose that the perpendicular distance to the wire is
using the Biot-Savart
law. Suppose that the perpendicular distance to the wire is 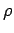 . It is
easily seen that
. It is
easily seen that
Thus, according to Eq. (339), we have
which gives the familiar result
 |
(345) |
So, we have come full circle in our investigation of magnetic fields.
Note that the simple result (345) can only be obtained from the Biot-Savart law
after some non-trivial algebra.
Examination of
more complicated current distributions using this law invariably
leads to lengthy, involved, and extremely unpleasant
calculations.



Next: Electrostatics and magnetostatics
Up: Time-independent Maxwell equations
Previous: The magnetic vector potential
Richard Fitzpatrick
2006-02-02
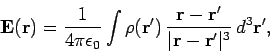
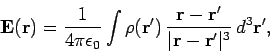
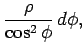


![$\displaystyle \frac{\mu_0 I}{4\pi \rho} \int_{-\pi/2}^{\pi/2} \cos\phi d\phi
= \frac{\mu_0 I}{4\pi \rho} \left[ \sin\phi\right]_{-\pi/2}^{\pi/2},$](img896.png)