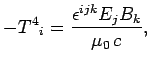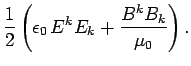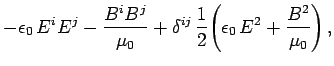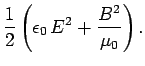Next: Accelerated charges
Up: Relativity and electromagnetism
Previous: The force on a
The electromagnetic energy tensor
Consider a continuous volume distribution of charged matter in the
presence of an electromagnetic field. Let there be  particles
per unit proper volume (unit volume determined in the local rest frame),
each carrying a charge
particles
per unit proper volume (unit volume determined in the local rest frame),
each carrying a charge 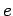 . Consider an inertial frame in which the
3-velocity field of the particles is
. Consider an inertial frame in which the
3-velocity field of the particles is 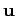 . The number density of the
particles in this frame is
. The number density of the
particles in this frame is
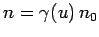 .
The charge density
and the 3-current due to the particles are
.
The charge density
and the 3-current due to the particles are 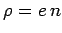 and
and
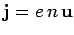 , respectively.
Multiplying Eq. (1564)
by the proper number density of particles,
, respectively.
Multiplying Eq. (1564)
by the proper number density of particles,  , we obtain an expression
, we obtain an expression
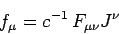 |
(1568) |
for the 4-force 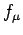 acting on unit proper volume of the distribution
due to the ambient electromagnetic fields. Here, we have made use of
the definition
acting on unit proper volume of the distribution
due to the ambient electromagnetic fields. Here, we have made use of
the definition
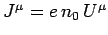 . It is easily demonstrated, using some of the
results obtained in the previous section, that
. It is easily demonstrated, using some of the
results obtained in the previous section, that
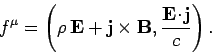 |
(1569) |
The above expression remains valid when there are many
charge species (e.g., electrons and ions) possessing different
number density and 3-velocity fields. The 4-vector 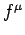 is
usually called the Lorentz force density.
is
usually called the Lorentz force density.
We know that Maxwell's equations reduce to
where  is the electromagnetic field tensor, and
is the electromagnetic field tensor, and
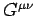 is its dual. As is easily verified, Eq. (1571)
can also be written in the form
is its dual. As is easily verified, Eq. (1571)
can also be written in the form
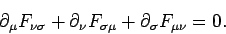 |
(1572) |
Equations (1568) and (1570) can be combined to give
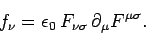 |
(1573) |
This expression can also be written
![\begin{displaymath}
f_\nu = \epsilon_0
\left[\partial_\mu(F^{\mu\sigma}F_{\nu\sigma})
-F^{\mu\sigma} \partial_\mu F_{\nu\sigma}\right].
\end{displaymath}](img3191.png) |
(1574) |
Now,
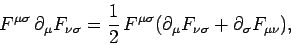 |
(1575) |
where use has been made of the antisymmetry of the electromagnetic
field tensor. It follows from Eq. (1572) that
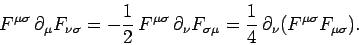 |
(1576) |
Thus,
![\begin{displaymath}
f_\nu =\epsilon_0 \left[\partial_\mu(F^{\mu\sigma}F_{\nu\sig...
...frac{1}{4} \partial_\nu (F^{\mu\sigma}F_{\mu\sigma})\right].
\end{displaymath}](img3194.png) |
(1577) |
The above expression can also be written
 |
(1578) |
where
![\begin{displaymath}
{T^\mu}_\nu = \epsilon_0\left[ F^{\mu\sigma}F_{\sigma\nu}
+ ...
...1}{4} \delta_\nu^\mu (F^{\rho\sigma}F_{\rho\sigma})\right]
\end{displaymath}](img3196.png) |
(1579) |
is called the electromagnetic energy tensor. Note that 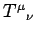 is a proper-4-tensor. It follows from Eqs. (1481), (1484), and (1516)
that
is a proper-4-tensor. It follows from Eqs. (1481), (1484), and (1516)
that
Equation (1578) can also be written
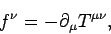 |
(1583) |
where  is a symmetric tensor whose elements are
is a symmetric tensor whose elements are
Consider the time-like component of Eq. (1583). It follows from Eq. (1569)
that
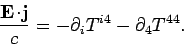 |
(1587) |
This equation can be rearranged to give
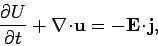 |
(1588) |
where 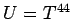 and
and
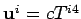 , so that
, so that
 |
(1589) |
and
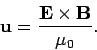 |
(1590) |
The right-hand side of Eq. (1588) represents the rate
per unit volume at which energy is
transferred from the
electromagnetic field to charged particles.
It is clear, therefore, that Eq. (1588) is an energy conservation
equation for the electromagnetic field (see Sect. 8.2). The proper-3-scalar 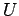 can be identified
as the energy density of the electromagnetic field, whereas
the proper-3-vector
can be identified
as the energy density of the electromagnetic field, whereas
the proper-3-vector 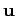 is the energy flux due to the electromagnetic field: i.e., the Poynting flux.
is the energy flux due to the electromagnetic field: i.e., the Poynting flux.
Consider the space-like components of Eq. (1583). It is easily demonstrated
that these reduce to
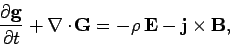 |
(1591) |
where
 and
and
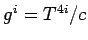 , or
, or
 |
(1592) |
and
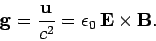 |
(1593) |
Equation (1591) is basically a momentum conservation equation for the
electromagnetic field (see Sect. 8.4). The right-hand side represents the rate per unit volume
at which momentum is transferred from the electromagnetic
field to charged particles. The
symmetric proper-3-tensor
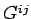 specifies the flux of electromagnetic
momentum parallel to the
specifies the flux of electromagnetic
momentum parallel to the 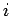 th axis crossing a surface
normal to the
th axis crossing a surface
normal to the 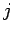 th axis. The proper-3-vector
th axis. The proper-3-vector 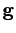 represents
the momentum density of the electromagnetic field. It is clear that
the energy conservation law (1588) and the momentum conservation law
(1591) can be combined together to give the relativistically invariant
energy-momentum conservation law (1583).
represents
the momentum density of the electromagnetic field. It is clear that
the energy conservation law (1588) and the momentum conservation law
(1591) can be combined together to give the relativistically invariant
energy-momentum conservation law (1583).



Next: Accelerated charges
Up: Relativity and electromagnetism
Previous: The force on a
Richard Fitzpatrick
2006-02-02