


Next: Electromagnetic radiation
Up: Electromagnetic energy and momentum
Previous: Electromagnetic momentum
Momentum conservation
It follows from Eqs. (1036) and (1050) that the momentum
density of electromagnetic fields can be written
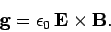 |
(1058) |
Now, a momentum conservation equation for electromagnetic fields
should take the integral form
![\begin{displaymath}
-\frac{\partial}{\partial t}\int_V g_i dV = \int_S G_{ij} ...
...int_V \left[\rho {\bf E} + {\bf j}\times{\bf B}\right]_i dV.
\end{displaymath}](img2168.png) |
(1059) |
Here, 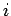 and
and 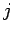 run from 1 to 3 (1 corresponds to the
run from 1 to 3 (1 corresponds to the 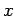 -direction,
2 to the
-direction,
2 to the 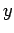 -direction, and 3 to the
-direction, and 3 to the 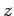 -direction). Moreover, the Einstein
summation convention is employed for repeated indices (e.g.,
-direction). Moreover, the Einstein
summation convention is employed for repeated indices (e.g.,
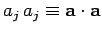 ). Furthermore, the tensor
). Furthermore, the tensor
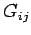 represents the flux of the
represents the flux of the 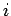 th component of electromagnetic momentum in the
th component of electromagnetic momentum in the 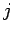 -direction. This tensor (a tensor is a direct generalization of a vector with two indices instead of one) is called
the momentum flux density. Hence, the above equation states
that the rate of loss of electromagnetic momentum in some volume
-direction. This tensor (a tensor is a direct generalization of a vector with two indices instead of one) is called
the momentum flux density. Hence, the above equation states
that the rate of loss of electromagnetic momentum in some volume  is equal to the flux of electromagnetic momentum across the bounding surface
is equal to the flux of electromagnetic momentum across the bounding surface  plus the rate at which momentum is transferred to matter inside
plus the rate at which momentum is transferred to matter inside  .
The latter rate is, of course, just the net electromagnetic force acting
on matter inside
.
The latter rate is, of course, just the net electromagnetic force acting
on matter inside  : i.e., the volume integral of the electromagnetic
force density,
: i.e., the volume integral of the electromagnetic
force density,
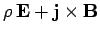 .
Now, a direct generalization of the divergence theorem states that
.
Now, a direct generalization of the divergence theorem states that
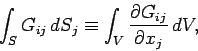 |
(1060) |
where 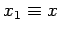 ,
, 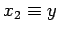 , etc. Hence, in differential form, our
momentum conservation equation for electromagnetic fields is written
, etc. Hence, in differential form, our
momentum conservation equation for electromagnetic fields is written
![\begin{displaymath}
-\frac{\partial}{\partial t}\left[\epsilon_0 {\bf E}\times{...
...ij}}{\partial x_j} + [\rho {\bf E} + {\bf j}\times{\bf B}]_i.
\end{displaymath}](img2175.png) |
(1061) |
Let us now attempt to derive an equation of this form from Maxwell's equations.
Maxwell's equations are written:
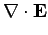 |
 |
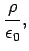 |
(1062) |
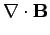 |
 |
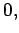 |
(1063) |
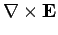 |
 |
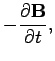 |
(1064) |
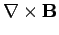 |
 |
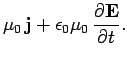 |
(1065) |
We can cross Eq. (1065) divided by 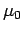 with
with 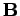 , and rearrange, to give
, and rearrange, to give
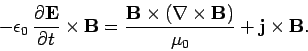 |
(1066) |
Next, let us cross 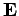 with Eq. (1064) times
with Eq. (1064) times 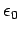 ,
rearrange, and add the result to the above equation. We obtain
,
rearrange, and add the result to the above equation. We obtain
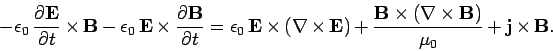 |
(1067) |
Next, making use of Eqs. (1062) and (1063), we get
Now, from vector field theory,
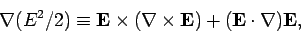 |
(1069) |
with a similar equation for 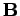 . Hence, Eq. (1068)
takes the form
. Hence, Eq. (1068)
takes the form
Finally, when written in terms of components, the above equation becomes
since
![$[(\nabla\cdot{\bf E}) {\bf E}]_i = (\partial E_j/\partial x_j) E_i$](img2189.png) ,
and
,
and
![$[({\bf E}\cdot\nabla){\bf E}]_i = E_j (\partial E_i/\partial x_j)$](img2190.png) .
Here,
.
Here, 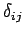 is a Kronecker delta symbol (i.e.,
is a Kronecker delta symbol (i.e., 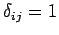 if
if 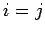 , and
, and 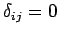 otherwise).
Comparing the above equation with Eq. (1061), we conclude that
the momentum flux density tensor of electromagnetic fields takes the
form
otherwise).
Comparing the above equation with Eq. (1061), we conclude that
the momentum flux density tensor of electromagnetic fields takes the
form
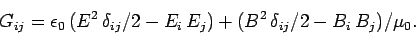 |
(1072) |
The momentum conservation equation (1061) is sometimes written
![\begin{displaymath}[\rho {\bf E} + {\bf j}\times{\bf B}]_i = \frac {\partial T_...
...l}{\partial t}\left[\epsilon_0 {\bf E}\times{\bf B}\right]_i,
\end{displaymath}](img2196.png) |
(1073) |
where
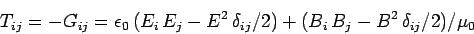 |
(1074) |
is called the Maxwell stress tensor.



Next: Electromagnetic radiation
Up: Electromagnetic energy and momentum
Previous: Electromagnetic momentum
Richard Fitzpatrick
2006-02-02
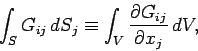
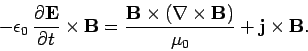
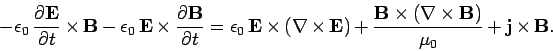
![$\displaystyle -\frac{\partial}{\partial t} \left[\epsilon_0 {\bf E}\times{\bf B}\right]$](img2179.png)
![$\displaystyle +\frac{1}{\mu_0}\left[\nabla(B^2/2) - (\nabla\cdot {\bf B}) {\bf B} - ({\bf B}\cdot\nabla){\bf B}\right]$](img2184.png)
![$\displaystyle -\frac{\partial}{\partial t} \left[\epsilon_0 {\bf E}\times{\bf B}\right]_i$](img2186.png)
![$\displaystyle \frac{\partial}{\partial x_j}\!\left[\epsilon_0 E^2 \delta_{ij}/2 - \epsilon_0 E_i E_j+ B^2 \delta_{ij}/2 \mu_0 - B_i B_j/\mu_0\right]$](img2187.png)
![\begin{displaymath}[\rho {\bf E} + {\bf j}\times{\bf B}]_i = \frac {\partial T_...
...l}{\partial t}\left[\epsilon_0 {\bf E}\times{\bf B}\right]_i,
\end{displaymath}](img2196.png)