

Next: Potential due to a
Up: Relativity and electromagnetism
Previous: The dual electromagnetic field
The electromagnetic field tensor transforms according to the standard
rule
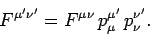 |
(1511) |
This easily yields the celebrated rules for transforming electromagnetic
fields:
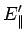 |
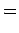 |
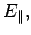 |
(1512) |
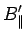 |
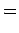 |
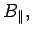 |
(1513) |
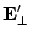 |
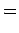 |
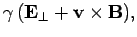 |
(1514) |
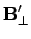 |
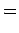 |
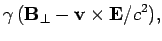 |
(1515) |
where 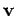 is the relative velocity between the primed and unprimed
frames, and the perpendicular and parallel directions are, respectively,
perpendicular and parallel to
is the relative velocity between the primed and unprimed
frames, and the perpendicular and parallel directions are, respectively,
perpendicular and parallel to 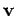 .
.
At this stage, we may conveniently note two important invariants of the
electromagnetic field. They are
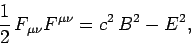 |
(1516) |
and
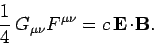 |
(1517) |
The first of these quantities is a proper-scalar, and the second
a pseudo-scalar.


Next: Potential due to a
Up: Relativity and electromagnetism
Previous: The dual electromagnetic field
Richard Fitzpatrick
2006-02-02