


Next: Fields due to a
Up: Relativity and electromagnetism
Previous: Transformation of fields
Potential due to a moving charge
Suppose that a particle carrying a charge 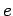 moves with uniform
velocity
moves with uniform
velocity 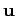 through a frame
through a frame  . Let us evaluate the
vector potential,
. Let us evaluate the
vector potential,  , and the scalar potential,
, and the scalar potential,  , due to
this charge at a given event
, due to
this charge at a given event  in
in  .
.
Let us choose coordinates in  so that
so that 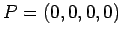 and
and
 . Let
. Let 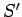 be that frame in the standard configuration
with respect to
be that frame in the standard configuration
with respect to  in which the charge is (permanently) at rest
at (say) the point
in which the charge is (permanently) at rest
at (say) the point 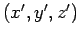 . In
. In 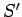 , the potential at
, the potential at  is the
usual potential due to a stationary charge,
is the
usual potential due to a stationary charge,
where
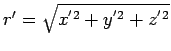 . Let us now transform
these equations directly into the frame
. Let us now transform
these equations directly into the frame  . Since
. Since
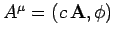 is a contravariant 4-vector, its components transform according to the
standard rules (1397)-(1400). Thus,
is a contravariant 4-vector, its components transform according to the
standard rules (1397)-(1400). Thus,
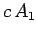 |
 |
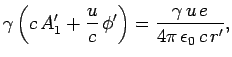 |
(1520) |
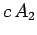 |
 |
 |
(1521) |
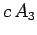 |
 |
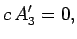 |
(1522) |
 |
 |
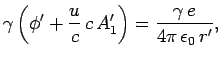 |
(1523) |
since  in this case. It remains to express the quantity
in this case. It remains to express the quantity 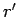 in terms of quantities measured in
in terms of quantities measured in  . The most physically meaningful
way of doing this is to express
. The most physically meaningful
way of doing this is to express 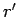 in terms of retarded values
in
in terms of retarded values
in  . Consider the retarded event at the charge for which, by definition,
. Consider the retarded event at the charge for which, by definition,
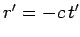 and
and 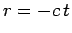 . Using the standard Lorentz transformation,
(1346)-(1349), we find that
. Using the standard Lorentz transformation,
(1346)-(1349), we find that
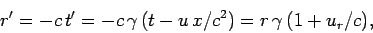 |
(1524) |
where
 denotes the radial
velocity of the change in
denotes the radial
velocity of the change in  . We can now rewrite Eqs. (1520)-(1523) in the
form
. We can now rewrite Eqs. (1520)-(1523) in the
form
where the square brackets, as usual, indicate that the enclosed quantities
must be retarded. For a uniformly moving charge, the retardation of
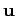 is, of course, superfluous.
However, since
is, of course, superfluous.
However, since
![\begin{displaymath}
{\mit\Phi}^\mu = \frac{1}{4\pi \epsilon_0 c}\int
\frac{[J^\mu]}{r} dV,
\end{displaymath}](img3124.png) |
(1527) |
it is clear that the potentials depend only on the (retarded) velocity
of the charge, and not on its acceleration. Consequently, the expressions
(1525) and (1526) give the correct potentials for an arbitrarily moving charge.
They are known as the Liénard-Wiechert potentials.



Next: Fields due to a
Up: Relativity and electromagnetism
Previous: Transformation of fields
Richard Fitzpatrick
2006-02-02
![]() so that
so that ![]() and
and
![]() . Let
. Let ![]() be that frame in the standard configuration
with respect to
be that frame in the standard configuration
with respect to ![]() in which the charge is (permanently) at rest
at (say) the point
in which the charge is (permanently) at rest
at (say) the point ![]() . In
. In ![]() , the potential at
, the potential at ![]() is the
usual potential due to a stationary charge,
is the
usual potential due to a stationary charge,
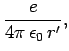
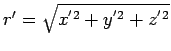 . Let us now transform
these equations directly into the frame
. Let us now transform
these equations directly into the frame ![\begin{displaymath}
{\mit\Phi}^\mu = \frac{1}{4\pi \epsilon_0 c}\int
\frac{[J^\mu]}{r} dV,
\end{displaymath}](img3124.png)