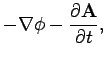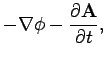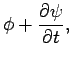Next: Retarded potentials
Up: Relativity and electromagnetism
Previous: The potential 4-vector
The electric and magnetic fields are obtained from the vector and
scalar potentials according to the prescription (see Sect. 4.3)
These fields are important, because they determine the electromagnetic forces
exerted on charged particles. Note that the above prescription does not
uniquely determine the two potentials. It is possible to make the
following transformation, known as a gauge transformation, which
leaves the fields unaltered (see Sect. 4.4):
where
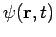 is a general scalar field. It is necessary
to adopt some form of convention, generally known as a gauge condition,
to fully specify the two potentials. In fact, there is only one gauge condition
which is consistent with Eqs. (1436). This is the Lorentz gauge
condition,
is a general scalar field. It is necessary
to adopt some form of convention, generally known as a gauge condition,
to fully specify the two potentials. In fact, there is only one gauge condition
which is consistent with Eqs. (1436). This is the Lorentz gauge
condition,
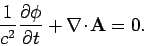 |
(1447) |
Note that this condition can be written in the Lorentz invariant form
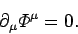 |
(1448) |
This implies that if the Lorentz gauge holds in one particular inertial
frame then it automatically holds in all
other inertial frames. A general gauge transformation
can be written
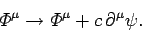 |
(1449) |
Note that even after the Lorentz gauge has been adopted, the potentials
are undetermined to a gauge transformation using a scalar field, 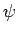 , which
satisfies the sourceless wave equation
, which
satisfies the sourceless wave equation
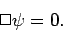 |
(1450) |
However, if we adopt sensible boundary conditions in both
space and time then the only solution to the above equation is 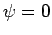 .
.



Next: Retarded potentials
Up: Relativity and electromagnetism
Previous: The potential 4-vector
Richard Fitzpatrick
2006-02-02