


Next: The potential 4-vector
Up: Relativity and electromagnetism
Previous: 4-velocity and 4-acceleration
Let us now consider the laws of electromagnetism. We wish to demonstrate
that these laws are compatible with the relativity principle. In order
to achieve this, it is necessary for us to make an assumption
about the transformation properties of electric charge. The assumption
we shall make, which is well substantiated experimentally, is that
charge, unlike mass, is invariant. That is, the charge carried by a
given particle has the same measure in all inertial frames.
In particular, the charge carried by a particle does not vary with
the particle's velocity.
Let us suppose, following Lorentz, that all charge is made up
of elementary particles, each carrying the invariant amount 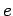 . Suppose
that
. Suppose
that 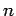 is the number density of such charges at some given point and
time, moving with velocity
is the number density of such charges at some given point and
time, moving with velocity 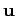 , as observed in a frame
, as observed in a frame  .
Let
.
Let  be the number density of charges in the frame
be the number density of charges in the frame 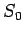 in which the
charges are momentarily at rest. As is well-known, a volume of measure
in which the
charges are momentarily at rest. As is well-known, a volume of measure
 in
in  has measure
has measure 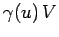 in
in 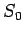 (because of length contraction).
Since observers in both frames must agree on how many particles are
contained in the volume, and, hence, on how much charge it contains, it
follows that
(because of length contraction).
Since observers in both frames must agree on how many particles are
contained in the volume, and, hence, on how much charge it contains, it
follows that
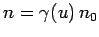 . If
. If 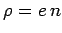 and
and 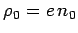 are
the charge densities in
are
the charge densities in  and
and 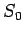 , respectively, then
, respectively, then
 |
(1431) |
The quantity 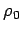 is called the proper density, and is obviously
Lorentz invariant.
is called the proper density, and is obviously
Lorentz invariant.
Suppose that 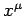 are the coordinates of the moving charge in
are the coordinates of the moving charge in  .
The current density 4-vector is constructed as follows:
.
The current density 4-vector is constructed as follows:
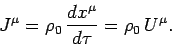 |
(1432) |
Thus,
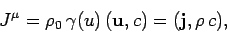 |
(1433) |
where
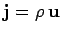 is the current density 3-vector. Clearly,
charge density and current density transform as the time-like and space-like
components of the same 4-vector.
is the current density 3-vector. Clearly,
charge density and current density transform as the time-like and space-like
components of the same 4-vector.
Consider the invariant 4-divergence of 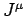 :
:
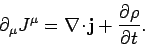 |
(1434) |
We know that one of the caveats of Maxwell's equations is the charge conservation law
 |
(1435) |
It is clear that this expression can be rewritten in the manifestly
Lorentz invariant form
 |
(1436) |
This equation tells us that there are no net sources or sinks of electric
charge in nature: i.e., electric charge is neither created nor
destroyed.



Next: The potential 4-vector
Up: Relativity and electromagnetism
Previous: 4-velocity and 4-acceleration
Richard Fitzpatrick
2006-02-02
![]() . Suppose
that
. Suppose
that ![]() is the number density of such charges at some given point and
time, moving with velocity
is the number density of such charges at some given point and
time, moving with velocity ![]() , as observed in a frame
, as observed in a frame ![]() .
Let
.
Let ![]() be the number density of charges in the frame
be the number density of charges in the frame ![]() in which the
charges are momentarily at rest. As is well-known, a volume of measure
in which the
charges are momentarily at rest. As is well-known, a volume of measure
![]() in
in ![]() has measure
has measure ![]() in
in ![]() (because of length contraction).
Since observers in both frames must agree on how many particles are
contained in the volume, and, hence, on how much charge it contains, it
follows that
(because of length contraction).
Since observers in both frames must agree on how many particles are
contained in the volume, and, hence, on how much charge it contains, it
follows that
![]() . If
. If ![]() and
and ![]() are
the charge densities in
are
the charge densities in ![]() and
and ![]() , respectively, then
, respectively, then
![]() are the coordinates of the moving charge in
are the coordinates of the moving charge in ![]() .
The current density 4-vector is constructed as follows:
.
The current density 4-vector is constructed as follows:
![]() :
: