Next: Potential outside uniform spheroid Up: Newtonian gravity Previous: Axially symmetric mass distributions
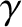 , and radius
, and radius 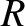 , whose center coincides with the origin. Expressing
, whose center coincides with the origin. Expressing
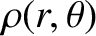 in the form of Equation (3.47), we find that
in the form of Equation (3.47), we find that
 |
(3.50) |
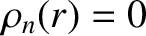 for
for 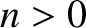 . Thus, from Equation (3.49),
. Thus, from Equation (3.49),
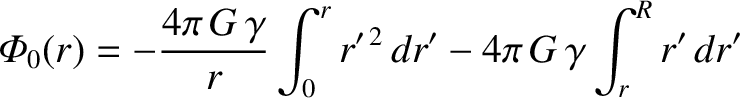 |
(3.51) |
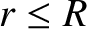 , and
, and
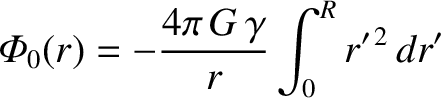 |
(3.52) |
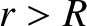 , with
, with
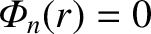 for
for 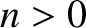 . Hence,
for
. Hence,
for 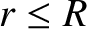 , and
for
, and
for 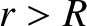 . Here,
. Here,
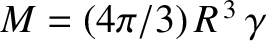 is the total mass of the sphere.
is the total mass of the sphere.
According to Equation (3.54), the gravitational potential outside a uniform sphere of mass  is the same as that generated by a point mass
is the same as that generated by a point mass  located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
preceding analysis, it is clear that
located
at the sphere's center. It turns out that this is a general result for any
finite spherically symmetric mass distribution.
Indeed, from the
preceding analysis, it is clear that
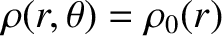 and
and
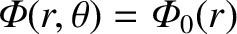 for such a distribution. Suppose that the
distribution extends out to
for such a distribution. Suppose that the
distribution extends out to 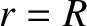 . It immediately follows, from Equation (3.49),
that
. It immediately follows, from Equation (3.49),
that
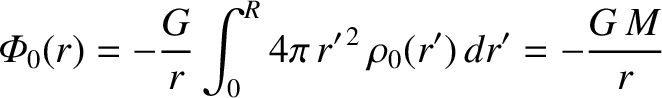 |
(3.55) |
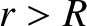 ,
where
,
where  is the total mass of the distribution.
is the total mass of the distribution.
Consider a point mass  that lies a distance
that lies a distance 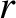 from the center of a spherically symmetric mass distribution of mass
from the center of a spherically symmetric mass distribution of mass
 (where
(where 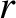 exceeds the outer radius of the distribution). Because the external gravitational potential generated by the distribution is the same as that of a point mass
exceeds the outer radius of the distribution). Because the external gravitational potential generated by the distribution is the same as that of a point mass  located at its center, the
force exerted on the mass
located at its center, the
force exerted on the mass  by the distribution is the same as that due to a point mass
by the distribution is the same as that due to a point mass  located at the center of the distribution. In other
words, the force is of magnitude
located at the center of the distribution. In other
words, the force is of magnitude
 , and is directed from the mass toward the center of the distribution.
Assuming that the system is isolated, the resultant force that the mass exerts on the distribution is of magnitude
, and is directed from the mass toward the center of the distribution.
Assuming that the system is isolated, the resultant force that the mass exerts on the distribution is of magnitude
 ,
and has a line of action directed from the center of the distribution towards the mass. (See Section 2.10, Exercise 3.) However, this
is the same as the force that the mass
,
and has a line of action directed from the center of the distribution towards the mass. (See Section 2.10, Exercise 3.) However, this
is the same as the force that the mass  would exert on a point mass
would exert on a point mass  located at the center of the distribution. Because
gravitational fields are superposable, we conclude that the resultant gravitational force acting on a spherically
symmetric mass distribution of mass
located at the center of the distribution. Because
gravitational fields are superposable, we conclude that the resultant gravitational force acting on a spherically
symmetric mass distribution of mass  situated in the gravitational field generated by
many point masses is the same as that which would act on a point mass
situated in the gravitational field generated by
many point masses is the same as that which would act on a point mass  located at the
center of the distribution.
located at the
center of the distribution.
The center of mass of a spherically symmetric mass distribution lies at the geometric center of the distribution. Moreover, the translational motion of the center of mass is analogous to that of a point particle, whose mass is equal to that of the whole distribution, moving under the action of the resultant external force. (See Section 2.6.) If the external force is due to a gravitational field then the resultant force is the same as that exerted by the field on a point particle, whose mass is that of the distribution, located at the center of mass. We thus conclude that Newton's laws of motion, in their primitive form, apply not only to point masses, but also to the translational motions of extended spherically symmetric mass distributions interacting via gravity (e.g., the Sun and the planets).