Surface harmonics and solid harmonics

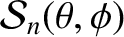A surface harmonic of degree (where is a non-negative integer), denoted ${\cal S}_n(\theta,\phi)$ , is defined as a well-behaved solution to

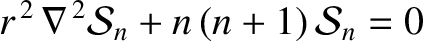$\displaystyle r^{\,2}\,\nabla^{\,2} {\cal S}_n + n\,(n+1)\,{\cal S}_n = 0$

(C.1)

on the surface of a sphere (i.e., constant). Here, 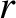, 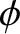$\theta$ , $\phi$ are standard spherical coordinates. It follows that

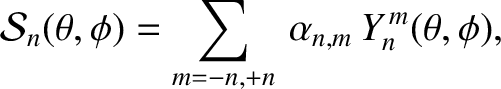$\displaystyle {\cal S}_n(\theta,\phi) = \sum_{m=-n,+n}\,\alpha_{n,m}\,Y_n^{\,m}(\theta,\phi),$

(C.2)

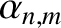where the $\alpha_{n,m}$ are arbitrary coefficients, and the $Y_n^{\,m}(\theta,\phi)$ are spherical harmonics. (See Section A.12.)

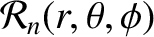A solid harmonic of degree (where is a non-negative integer), denoted ${\cal R}_n(r,\theta,\phi)$ , is defined as a well-behaved solution to

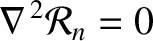$\displaystyle \nabla^{\,2} {\cal R}_n = 0$

(C.3)

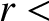in the interior of a sphere (i.e., the region constant). It follows that (Riley 1974c)

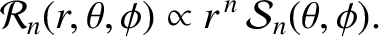$\displaystyle {\cal R}_n(r,\theta,\phi) \propto r^{\,n}\,{\cal S}_n(\theta,\phi).$

(C.4)

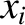Note that the Cartesian coordinates (where 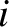runs from 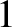to 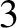) are solid harmonics of degree 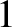. Moreover, 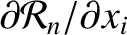$\partial {\cal R}_n/\partial x_i$ is a solid harmonic of degree 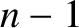. Here, we have employed standard tensor notation (Riley 1974e).

The following results regarding solid harmonics are helpful:

$\displaystyle x_i\,\frac{\partial {\cal R}_n}{\partial x_i}$	$\displaystyle = r\,\frac{\partial {\cal R}_n}{\partial r} = n\,{\cal R}_n,$	(C.5)
$\displaystyle \nabla^{\,2}(x_i\,{\cal R}_n)$	$\displaystyle = \nabla\cdot({\cal R}_n\,\nabla x_i + x_i\,\nabla{\cal R}_n) = 2\,\nabla x_i\cdot\nabla{\cal R}_n = 2\,\frac{\partial {\cal R}_n}{\partial x_i},$	(C.6)
$\displaystyle \nabla^{\,2}(r^{\,m}\,{\cal R}_n)$	$\displaystyle = \nabla^{\,2}(r^{\,m+n}\,{\cal S}_n) = \frac{1}{r^{\,2}}\,\frac{... ...,\frac{d}{dr}(r^{\,m+n}\,{\cal S}_n)\right] - n\,(n+1)\,r^{\,m+n-2}\,{\cal S}_n$
	$\displaystyle = m\,(m+2\,n+1)\,r^{\,m-2}\,{\cal R}_n.$	(C.7)

In deriving these results, use has been made of standard vector field theory (Fitzpatrick 2008). In addition, we have adopted the well-known Einstein summation convention that repeated indices are implicitly summed from 1 to 3 (Riley 1974e).