Consider a spherical planet whose unperturbed surface corresponds to  . Suppose that this planet is
subject to a small, externally generated, tidal potential
. Suppose that this planet is
subject to a small, externally generated, tidal potential
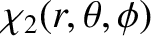 , where
, where  is a solid harmonic of degree 2.
The planet is modeled as a solid body of uniform mass density
is a solid harmonic of degree 2.
The planet is modeled as a solid body of uniform mass density 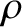 whose perturbed surface lies at
whose perturbed surface lies at
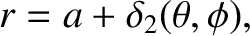 |
(C.8) |
where 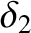 is a surface harmonic of degree 2. It is assumed that
is a surface harmonic of degree 2. It is assumed that
 .
.
The net gravitational acceleration in the vicinity of the planet takes the form
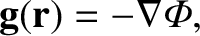 |
(C.9) |
where
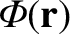 is the gravitational potential.
According to standard gravitational theory,
is the gravitational potential.
According to standard gravitational theory,
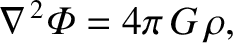 |
(C.10) |
where
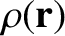 is the mass density distribution.
Thus, we can write
is the mass density distribution.
Thus, we can write
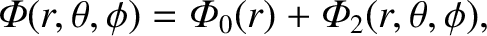 |
(C.11) |
where
![\begin{displaymath}\nabla^{\,2}{\mit\Phi}_0 \simeq\left\{
\begin{array}{lll} 4\p...
...mbox{\hspace{0.5cm}}&r\leq a\\ [0.5ex]
0r>a
\end{array}\right.,\end{displaymath}](img4234.png) |
(C.12) |
and
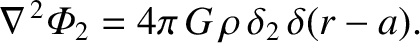 |
(C.13) |
[See Equations (E.2) and (E.3).]
Here,
 is a Dirac delta function (Riley 1974b).
The physical boundary conditions are
as
is a Dirac delta function (Riley 1974b).
The physical boundary conditions are
as
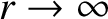 .
As is well known, the solutions to Laplace's equation,
.
As is well known, the solutions to Laplace's equation,
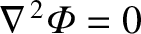 ,
take the general form
,
take the general form
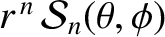 and
and
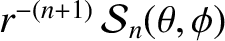 . Moreover, the
axisymmetric solution to
. Moreover, the
axisymmetric solution to
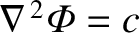 that is well behaved at the origin is
that is well behaved at the origin is
 .
(Riley 1974c.)
It follows that
and
where
.
(Riley 1974c.)
It follows that
and
where
 |
(C.20) |
is the gravitational acceleration at the planet's surface. Note that
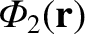 is a solid harmonic of degree 2 inside the planet (i.e.,
is a solid harmonic of degree 2 inside the planet (i.e., 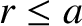 ).
).
 . Suppose that this planet is
subject to a small, externally generated, tidal potential
. Suppose that this planet is
subject to a small, externally generated, tidal potential
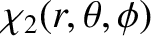 , where
, where  is a solid harmonic of degree 2.
The planet is modeled as a solid body of uniform mass density
is a solid harmonic of degree 2.
The planet is modeled as a solid body of uniform mass density 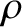 whose perturbed surface lies at
where
whose perturbed surface lies at
where 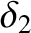 is a surface harmonic of degree 2. It is assumed that
is a surface harmonic of degree 2. It is assumed that
 .
.
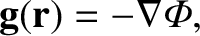
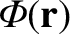 is the gravitational potential.
According to standard gravitational theory,
is the gravitational potential.
According to standard gravitational theory,
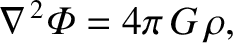
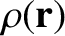 is the mass density distribution.
Thus, we can write
where
is the mass density distribution.
Thus, we can write
where
![\begin{displaymath}\nabla^{\,2}{\mit\Phi}_0 \simeq\left\{
\begin{array}{lll} 4\p...
...mbox{\hspace{0.5cm}}&r\leq a\\ [0.5ex]
0r>a
\end{array}\right.,\end{displaymath}](img4234.png)
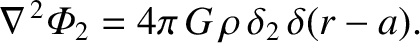
 is a Dirac delta function (Riley 1974b).
The physical boundary conditions are
is a Dirac delta function (Riley 1974b).
The physical boundary conditions are
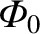
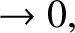
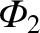
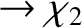
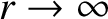 .
As is well known, the solutions to Laplace's equation,
.
As is well known, the solutions to Laplace's equation,
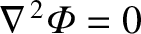 ,
take the general form
,
take the general form
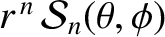 and
and
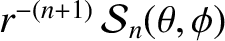 . Moreover, the
axisymmetric solution to
. Moreover, the
axisymmetric solution to
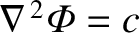 that is well behaved at the origin is
that is well behaved at the origin is
 .
(Riley 1974c.)
It follows that
and
.
(Riley 1974c.)
It follows that
and
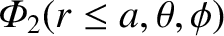
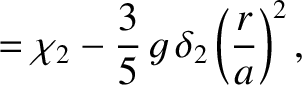
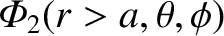
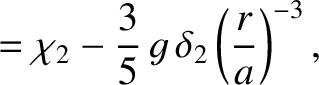

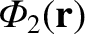 is a solid harmonic of degree 2 inside the planet (i.e.,
is a solid harmonic of degree 2 inside the planet (i.e., 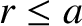 ).
).