Effect of solar radiation on interplanetary dust grains
An interplanetary dust grain orbiting the Sun absorbs solar radiation, and immediately re-radiates the absorbed energy isotropically in its instantaneous rest frame.
(Here, we are assuming that the size of the grain is much larger than the wavelength of the radiation, and, also,
that the grain is rapidly rotating, so the radiative heating of its surface is even.) Because the angular distributions
of the absorbed and emitted radiation patterns are different, and because
electromagnetic radiation possesses momentum (Fitzpatrick 2008), a net radiation pressure force is exerted on the grain.
Although this force is very small, when integrated over a sufficiently long period of time, it can significantly modify the dust grain orbit, causing the
grain to spiral in toward the Sun. Let us investigate this effect.
Let 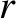 ,
, 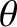 ,
, 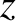 be cylindrical polar coordinates in a frame of reference, centered on the Sun, that is aligned with the orbital
plane of the dust grain, as
described in Section I.1. Let
be cylindrical polar coordinates in a frame of reference, centered on the Sun, that is aligned with the orbital
plane of the dust grain, as
described in Section I.1. Let 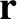 and
and
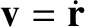 be the (relative) position and velocity of the grain, respectively.
Consider a photon emitted by the Sun. Let
be the (relative) position and velocity of the grain, respectively.
Consider a photon emitted by the Sun. Let 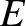 and
and 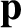 be the photon's energy and momentum, respectively, in the
heliocentric frame. Let
be the photon's energy and momentum, respectively, in the
heliocentric frame. Let 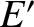 and
and 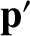 be the corresponding quantities in the dust grain's instantaneous rest frame.
According to standard relativistic theory (Rindler 1977),
be the corresponding quantities in the dust grain's instantaneous rest frame.
According to standard relativistic theory (Rindler 1977),
where
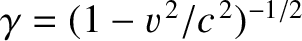 .
Assuming that the grain is moving non-relativistically, so that
.
Assuming that the grain is moving non-relativistically, so that 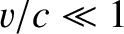 , the previous
expressions reduce to
respectively, to first order in
, the previous
expressions reduce to
respectively, to first order in 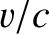 . The corresponding inverse transforms are
To first order in
. The corresponding inverse transforms are
To first order in 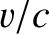 , the previous four expressions also apply to energy and momentum measured per unit time.
, the previous four expressions also apply to energy and momentum measured per unit time.
Let
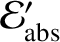 and
and
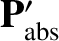 be the electromagnetic energy and momentum, respectively, absorbed by the
grain per unit time in its instantaneous rest frame. Let
be the electromagnetic energy and momentum, respectively, absorbed by the
grain per unit time in its instantaneous rest frame. Let
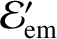 and
and
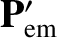 be the corresponding quantities emitted by the
grain.
Now, we are assuming that
be the corresponding quantities emitted by the
grain.
Now, we are assuming that
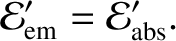 |
(10.166) |
In other words, all energy absorbed by the grain is immediately re-emitted. We also assuming that
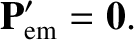 |
(10.167) |
In other words, the emitted radiation pattern is isotropic in the grain's instantaneous rest frame, and consequently carries off zero
net momentum.
It follows that the grain's net rate of energy gain in its instantaneous rest frame is
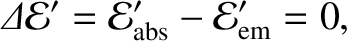 |
(10.168) |
whereas the corresponding rate of momentum gain is
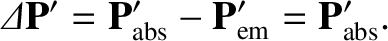 |
(10.169) |
Transforming to the heliocentric frame, we obtain
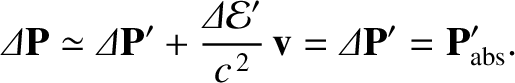 |
(10.170) |
where use has been made of Equations (10.165), (10.168), and (10.169).
However, according to Equation (10.163),
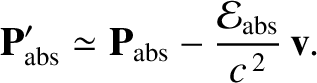 |
(10.171) |
Furthermore,
to first order in 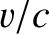 ,
where
,
where 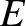 is the mean energy of a photon emitted by the Sun,
is the mean energy of a photon emitted by the Sun,
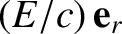 the corresponding mean momentum (Rindler 1977),
the corresponding mean momentum (Rindler 1977), 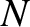 the local photon number density, and
the local photon number density, and  the cross-sectional
area of the grain (normal to
the cross-sectional
area of the grain (normal to 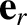 ).
It follows that, to first order in
).
It follows that, to first order in 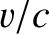 ,
,
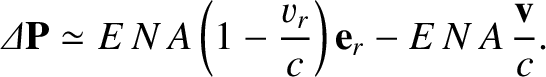 |
(10.174) |
Of course,
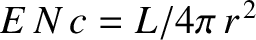 is the local solar electromagnetic energy flux, where
is the local solar electromagnetic energy flux, where
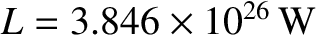 is the solar luminosity (Yoder 1995).
is the solar luminosity (Yoder 1995).
In the heliocentric frame, the net force per unit mass acting on the grain is
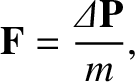 |
(10.175) |
where 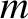 is the grain's mass. It follows from the previous analysis that
is the grain's mass. It follows from the previous analysis that
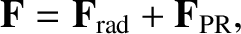 |
(10.176) |
where
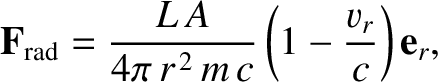 |
(10.177) |
and
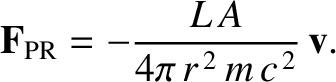 |
(10.178) |
[A more rigorous derivation of the previous two equations is given in Robertson 1937 and Klačka 1993.]
Here,
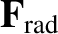 is the radiation pressure force per se, and is everywhere directed radially outward from the Sun.
On the other hand,
is the radiation pressure force per se, and is everywhere directed radially outward from the Sun.
On the other hand,
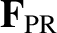 is the so-called Poynting-Robertson drag, and is always oppositely directed to the
grain's instantaneous velocity (Poynting 1904; Robertson 1937). The origin of
the latter force, which is much smaller in magnitude than the former, is the slightly non-isotropic angular distribution of the radiation re-emitted by the
grain, as seen in the Sun's rest frame. Finally, if we write
is the so-called Poynting-Robertson drag, and is always oppositely directed to the
grain's instantaneous velocity (Poynting 1904; Robertson 1937). The origin of
the latter force, which is much smaller in magnitude than the former, is the slightly non-isotropic angular distribution of the radiation re-emitted by the
grain, as seen in the Sun's rest frame. Finally, if we write
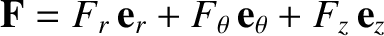 then the
previous three equations imply that
where use has been made of Equations (I.3), (I.7), and (I.10).
then the
previous three equations imply that
where use has been made of Equations (I.3), (I.7), and (I.10).
Assuming that the total radiation pressure force, (10.176), is small compared to the force of gravitational attraction between the Sun and the
dust grain—and can, thus, be treated as a perturbation—the grain's orbit can be modeled as Keplerian ellipse whose six elements evolve
slowly in time under the influence of the pressure. The six elements in question are chosen to be the major radius,  , the mean anomaly at epoch,
, the mean anomaly at epoch,
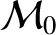 , the eccentricity,
, the eccentricity, 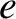 , the argument of the perigee,
, the argument of the perigee, 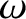 ,
the inclination (to the ecliptic plane),
,
the inclination (to the ecliptic plane), 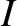 , and the longitude of the ascending node (measured with respect to the vernal equinox),
, and the longitude of the ascending node (measured with respect to the vernal equinox),
 .
(See Section 4.12.) The evolution of these elements is governed by the Gauss planetary equations, (I.53)–(I.58). Now, in the perturbative limit, the evolution of the dust grain's orbital elements takes place on a timescale that is
much longer than its orbital period. We can concentrate on this evolution, and filter out any
relatively short-term oscillations in the elements, by averaging the Gauss planetary equations over an
orbital period.
A suitable orbit-average operator is
.
(See Section 4.12.) The evolution of these elements is governed by the Gauss planetary equations, (I.53)–(I.58). Now, in the perturbative limit, the evolution of the dust grain's orbital elements takes place on a timescale that is
much longer than its orbital period. We can concentrate on this evolution, and filter out any
relatively short-term oscillations in the elements, by averaging the Gauss planetary equations over an
orbital period.
A suitable orbit-average operator is
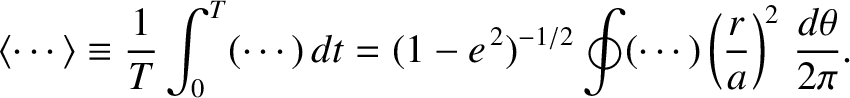 |
(10.182) |
Here, we have made use of the fact that
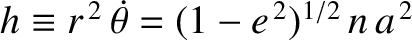 is a constant of the unperturbed motion. (See Chapter 4.) Note
that
is a constant of the unperturbed motion. (See Chapter 4.) Note
that
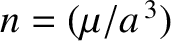 is the unperturbed mean orbital angular velocity. Moreover,
is the unperturbed mean orbital angular velocity. Moreover, 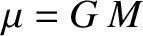 , where
, where  is the solar mass. (Of course, we are ignoring the
mass of the grain with respect to that of the Sun.)
Making use of Equations (10.179)–(10.181), as well as some of the formulae appearing in Appendix I,
the orbit-averaged Gauss planetary equations become
It can be seen that the radiation pressure force causes the grain's orbital major radius and eccentricity to both decrease monotonically
in time [because the left-hand sides of Equations (10.183) and (10.185) are both negative.]
On the other hand, radiation pressure has no effect on the either the location of the grain's perihelion point or the orientation of its orbital plane (because
is the solar mass. (Of course, we are ignoring the
mass of the grain with respect to that of the Sun.)
Making use of Equations (10.179)–(10.181), as well as some of the formulae appearing in Appendix I,
the orbit-averaged Gauss planetary equations become
It can be seen that the radiation pressure force causes the grain's orbital major radius and eccentricity to both decrease monotonically
in time [because the left-hand sides of Equations (10.183) and (10.185) are both negative.]
On the other hand, radiation pressure has no effect on the either the location of the grain's perihelion point or the orientation of its orbital plane (because
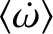 ,
,
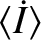 and
and
 are all zero).
Finally, given that the right-hand side of Equation (10.184) is negative, the radiation pressure force produces a slight reduction in the grain's mean orbital angular velocity: the modified
angular velocity being
are all zero).
Finally, given that the right-hand side of Equation (10.184) is negative, the radiation pressure force produces a slight reduction in the grain's mean orbital angular velocity: the modified
angular velocity being
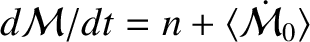 .
Note that, to lowest order in
.
Note that, to lowest order in 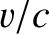 , the radial radiation pressure force,
, the radial radiation pressure force,
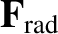 , averages out of the expressions for
, averages out of the expressions for
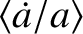 and
and
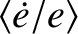 . Hence, the reduction in the grain's orbital major radius and eccentricity is due to the
Poynting-Robertson drag,
. Hence, the reduction in the grain's orbital major radius and eccentricity is due to the
Poynting-Robertson drag,
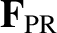 , combined with the first-order component of
, combined with the first-order component of
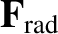 . (
. (
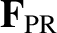 is similar in magnitude to the first-order component of
is similar in magnitude to the first-order component of
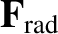 .) On the other hand, the
lowest-order component of
.) On the other hand, the
lowest-order component of
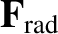 makes the dominant contribution to the
expression for
makes the dominant contribution to the
expression for
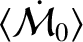 (in fact, we have neglected any first-order contributions to this expression).
(in fact, we have neglected any first-order contributions to this expression).
In order to be in the perturbative limit, the
relative changes in the dust grain's orbital elements induced by the radiation pressure force in an orbital period must all be small.
Because
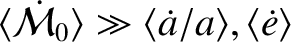 [given that
[given that
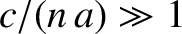 , which follows because the grain is moving non-relativistically], this requirement yields
, which follows because the grain is moving non-relativistically], this requirement yields
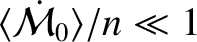 , or
, or
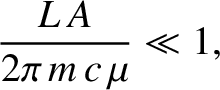 |
(10.189) |
which is equivalent to the requirement that the radiation pressure force be much smaller than the force of gravitational attraction between the grain and the Sun.
Let us model the grain as a sphere of radius 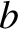 and mass density
and mass density 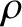 . It follows that
. It follows that
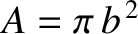 and
and
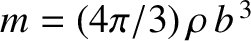 .
Thus, the previous expression yields
.
Thus, the previous expression yields
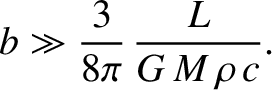 |
(10.190) |
Given that
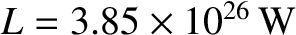 ,
,
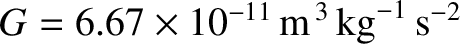 ,
,
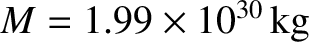 ,
,
 (Yoder 1995), and assuming that
(Yoder 1995), and assuming that
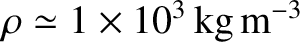 , we obtain
, we obtain
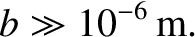 |
(10.191) |
We conclude that the radiation pressure force is perturbative for “large” dust grains whose radii are much greater than a micron. On the
other hand, the radiation pressure force—whose dominant component is directed radially outward from the Sun—exceeds the force of gravitational attraction for “small” dust grains whose radii are less than, or of order, a micron. We
would, therefore, expect radiation pressure to eventually expel small dust grains from the solar system.
For the case of a large dust grain in a circular orbit around the Sun, Equation (10.183) gives
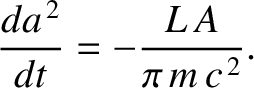 |
(10.192) |
Hence, the time required for a grain whose orbit has an initial radius  to spiral into the Sun is
to spiral into the Sun is
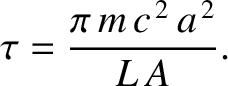 |
(10.193) |
Again modeling the grain as a sphere of radius 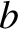 and mass density
and mass density
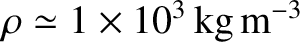 , we obtain
, we obtain
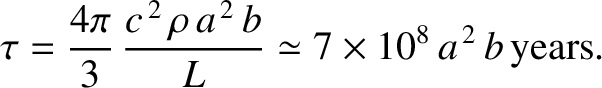 |
(10.194) |
Here,  is measured in astronomical units, and
is measured in astronomical units, and 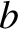 in meters. Thus, a dust grain of radius
in meters. Thus, a dust grain of radius
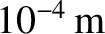 , and initial orbital
radius 1 AU, takes about
, and initial orbital
radius 1 AU, takes about 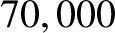 years to spiral into the Sun.
years to spiral into the Sun.
 ,
, 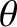 ,
, 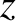 be cylindrical polar coordinates in a frame of reference, centered on the Sun, that is aligned with the orbital
plane of the dust grain, as
described in Section I.1. Let
be cylindrical polar coordinates in a frame of reference, centered on the Sun, that is aligned with the orbital
plane of the dust grain, as
described in Section I.1. Let 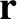 and
and
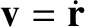 be the (relative) position and velocity of the grain, respectively.
Consider a photon emitted by the Sun. Let
be the (relative) position and velocity of the grain, respectively.
Consider a photon emitted by the Sun. Let 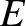 and
and 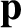 be the photon's energy and momentum, respectively, in the
heliocentric frame. Let
be the photon's energy and momentum, respectively, in the
heliocentric frame. Let 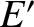 and
and 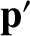 be the corresponding quantities in the dust grain's instantaneous rest frame.
According to standard relativistic theory (Rindler 1977),
be the corresponding quantities in the dust grain's instantaneous rest frame.
According to standard relativistic theory (Rindler 1977),
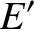
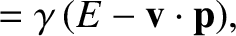
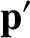
![$\displaystyle = {\bf p} +\left[(\gamma-1)\,\frac{{\bf v}\cdot{\bf p}}{v^{\,2}}-\frac{\gamma\,E}{c^{\,2}}\right]{\bf v},$](img2789.png)
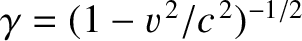 .
Assuming that the grain is moving non-relativistically, so that
.
Assuming that the grain is moving non-relativistically, so that 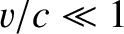 , the previous
expressions reduce to
, the previous
expressions reduce to
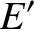
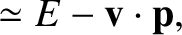
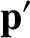
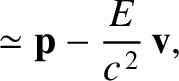
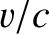 . The corresponding inverse transforms are
. The corresponding inverse transforms are
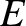
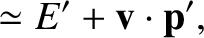
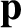
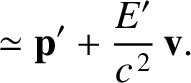
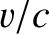 , the previous four expressions also apply to energy and momentum measured per unit time.
, the previous four expressions also apply to energy and momentum measured per unit time.
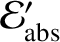 and
and
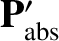 be the electromagnetic energy and momentum, respectively, absorbed by the
grain per unit time in its instantaneous rest frame. Let
be the electromagnetic energy and momentum, respectively, absorbed by the
grain per unit time in its instantaneous rest frame. Let
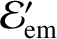 and
and
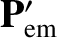 be the corresponding quantities emitted by the
grain.
Now, we are assuming that
be the corresponding quantities emitted by the
grain.
Now, we are assuming that
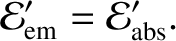
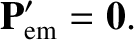
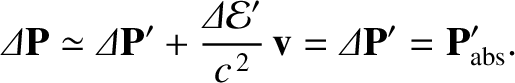
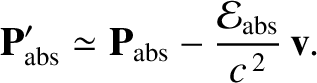
 ,
,
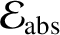
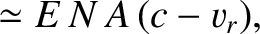
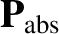
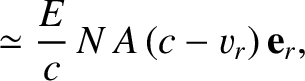
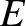 is the mean energy of a photon emitted by the Sun,
is the mean energy of a photon emitted by the Sun,
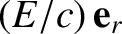 the corresponding mean momentum (Rindler 1977),
the corresponding mean momentum (Rindler 1977), 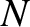 the local photon number density, and
the local photon number density, and  the cross-sectional
area of the grain (normal to
the cross-sectional
area of the grain (normal to 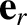 ).
It follows that, to first order in
).
It follows that, to first order in 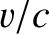 ,
,
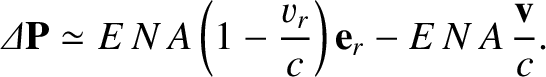
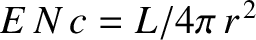 is the local solar electromagnetic energy flux, where
is the local solar electromagnetic energy flux, where
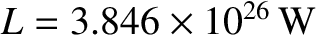 is the solar luminosity (Yoder 1995).
is the solar luminosity (Yoder 1995).
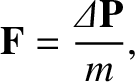
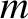 is the grain's mass. It follows from the previous analysis that
where
is the grain's mass. It follows from the previous analysis that
where
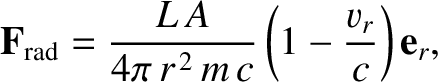
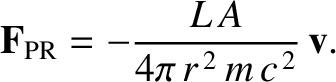
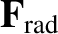 is the radiation pressure force per se, and is everywhere directed radially outward from the Sun.
On the other hand,
is the radiation pressure force per se, and is everywhere directed radially outward from the Sun.
On the other hand,
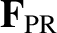 is the so-called Poynting-Robertson drag, and is always oppositely directed to the
grain's instantaneous velocity (Poynting 1904; Robertson 1937). The origin of
the latter force, which is much smaller in magnitude than the former, is the slightly non-isotropic angular distribution of the radiation re-emitted by the
grain, as seen in the Sun's rest frame. Finally, if we write
is the so-called Poynting-Robertson drag, and is always oppositely directed to the
grain's instantaneous velocity (Poynting 1904; Robertson 1937). The origin of
the latter force, which is much smaller in magnitude than the former, is the slightly non-isotropic angular distribution of the radiation re-emitted by the
grain, as seen in the Sun's rest frame. Finally, if we write
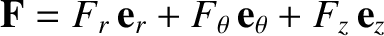 then the
previous three equations imply that
where use has been made of Equations (I.3), (I.7), and (I.10).
then the
previous three equations imply that
where use has been made of Equations (I.3), (I.7), and (I.10).
 , the mean anomaly at epoch,
, the mean anomaly at epoch,
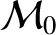 , the eccentricity,
, the eccentricity, 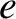 , the argument of the perigee,
, the argument of the perigee, 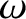 ,
the inclination (to the ecliptic plane),
,
the inclination (to the ecliptic plane), 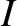 , and the longitude of the ascending node (measured with respect to the vernal equinox),
, and the longitude of the ascending node (measured with respect to the vernal equinox),
 .
(See Section 4.12.) The evolution of these elements is governed by the Gauss planetary equations, (I.53)–(I.58). Now, in the perturbative limit, the evolution of the dust grain's orbital elements takes place on a timescale that is
much longer than its orbital period. We can concentrate on this evolution, and filter out any
relatively short-term oscillations in the elements, by averaging the Gauss planetary equations over an
orbital period.
A suitable orbit-average operator is
.
(See Section 4.12.) The evolution of these elements is governed by the Gauss planetary equations, (I.53)–(I.58). Now, in the perturbative limit, the evolution of the dust grain's orbital elements takes place on a timescale that is
much longer than its orbital period. We can concentrate on this evolution, and filter out any
relatively short-term oscillations in the elements, by averaging the Gauss planetary equations over an
orbital period.
A suitable orbit-average operator is
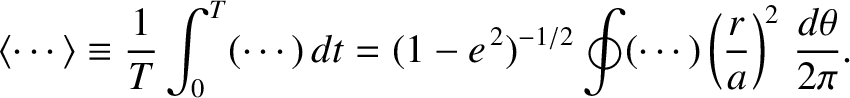
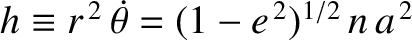 is a constant of the unperturbed motion. (See Chapter 4.) Note
that
is a constant of the unperturbed motion. (See Chapter 4.) Note
that
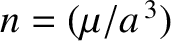 is the unperturbed mean orbital angular velocity. Moreover,
is the unperturbed mean orbital angular velocity. Moreover, 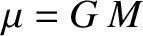 , where
, where  is the solar mass. (Of course, we are ignoring the
mass of the grain with respect to that of the Sun.)
Making use of Equations (10.179)–(10.181), as well as some of the formulae appearing in Appendix I,
the orbit-averaged Gauss planetary equations become
It can be seen that the radiation pressure force causes the grain's orbital major radius and eccentricity to both decrease monotonically
in time [because the left-hand sides of Equations (10.183) and (10.185) are both negative.]
On the other hand, radiation pressure has no effect on the either the location of the grain's perihelion point or the orientation of its orbital plane (because
is the solar mass. (Of course, we are ignoring the
mass of the grain with respect to that of the Sun.)
Making use of Equations (10.179)–(10.181), as well as some of the formulae appearing in Appendix I,
the orbit-averaged Gauss planetary equations become
It can be seen that the radiation pressure force causes the grain's orbital major radius and eccentricity to both decrease monotonically
in time [because the left-hand sides of Equations (10.183) and (10.185) are both negative.]
On the other hand, radiation pressure has no effect on the either the location of the grain's perihelion point or the orientation of its orbital plane (because
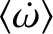 ,
,
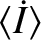 and
and
 are all zero).
Finally, given that the right-hand side of Equation (10.184) is negative, the radiation pressure force produces a slight reduction in the grain's mean orbital angular velocity: the modified
angular velocity being
are all zero).
Finally, given that the right-hand side of Equation (10.184) is negative, the radiation pressure force produces a slight reduction in the grain's mean orbital angular velocity: the modified
angular velocity being
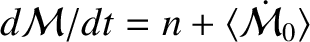 .
Note that, to lowest order in
.
Note that, to lowest order in 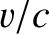 , the radial radiation pressure force,
, the radial radiation pressure force,
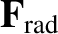 , averages out of the expressions for
, averages out of the expressions for
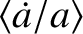 and
and
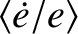 . Hence, the reduction in the grain's orbital major radius and eccentricity is due to the
Poynting-Robertson drag,
. Hence, the reduction in the grain's orbital major radius and eccentricity is due to the
Poynting-Robertson drag,
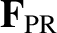 , combined with the first-order component of
, combined with the first-order component of
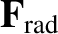 . (
. (
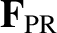 is similar in magnitude to the first-order component of
is similar in magnitude to the first-order component of
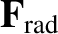 .) On the other hand, the
lowest-order component of
.) On the other hand, the
lowest-order component of
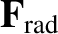 makes the dominant contribution to the
expression for
makes the dominant contribution to the
expression for
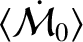 (in fact, we have neglected any first-order contributions to this expression).
(in fact, we have neglected any first-order contributions to this expression).
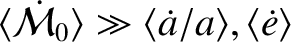 [given that
[given that
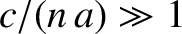 , which follows because the grain is moving non-relativistically], this requirement yields
, which follows because the grain is moving non-relativistically], this requirement yields
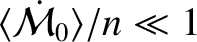 , or
, or
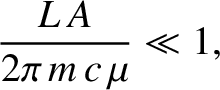
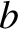 and mass density
and mass density 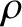 . It follows that
. It follows that
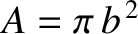 and
and
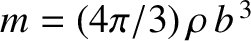 .
Thus, the previous expression yields
.
Thus, the previous expression yields
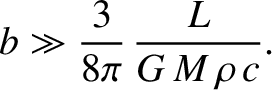
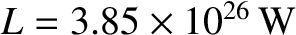 ,
,
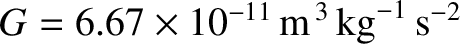 ,
,
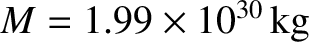 ,
,
 (Yoder 1995), and assuming that
(Yoder 1995), and assuming that
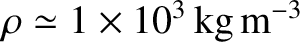 , we obtain
, we obtain
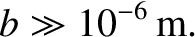
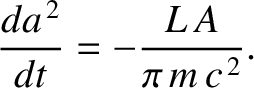
 to spiral into the Sun is
to spiral into the Sun is
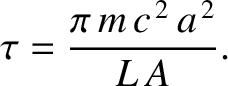
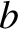 and mass density
and mass density
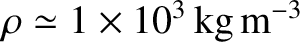 , we obtain
, we obtain
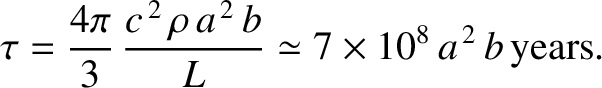
 is measured in astronomical units, and
is measured in astronomical units, and 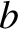 in meters. Thus, a dust grain of radius
in meters. Thus, a dust grain of radius
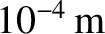 , and initial orbital
radius 1 AU, takes about
, and initial orbital
radius 1 AU, takes about 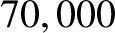 years to spiral into the Sun.
years to spiral into the Sun.