Next: Bibliography Up: Derivation of Gauss planetary Previous: Perturbed orbit in standard
 ; the mean anomaly at epoch,
; the mean anomaly at epoch,
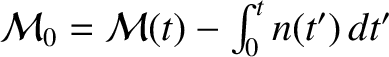 ; the eccentricity,
; the eccentricity,  ; the argument of the perihelion,
; the argument of the perihelion,  ;
the inclination to the ecliptic,
;
the inclination to the ecliptic,  ; and the longitude of the ascending node,
; and the longitude of the ascending node,
 . In the absence of a disturbing force,
. In the absence of a disturbing force,  ,
,
 ,
,  ,
,
 ,
,  , and
, and
 are all constants of the motion.
As is clear from the analysis of the preceding two sections, in the presence of a disturbing force of the form (I.15), the osculating elements evolve in time as follows:
These equations are known collectively as the Gauss planetary equations.
are all constants of the motion.
As is clear from the analysis of the preceding two sections, in the presence of a disturbing force of the form (I.15), the osculating elements evolve in time as follows:
These equations are known collectively as the Gauss planetary equations.