Suppose that the planet is subject to a perturbing force per unit mass, 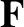 . Consequently, the planet's perturbed equation of motion becomes
. Consequently, the planet's perturbed equation of motion becomes
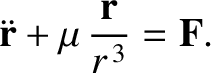 |
(I.14) |
We can write
 |
(I.15) |
The perturbing force causes the planet's orbital energy per unit mass to evolve in time as
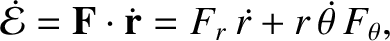 |
(I.16) |
where use has been made of Equations (I.3) and (I.15). Thus, it
follows from Equations (I.5), (I.7), (I.9), and (I.10) that
![$\displaystyle \frac{\skew{3}\dot{a}}{a} = \frac{2\,h}{\mu\,(1-e^{\,2})}\left[e\,\sin\theta\,F_r + (1+e\,\cos\theta)\,F_\theta\right].$](img5095.png) |
(I.17) |
The perturbing force causes the planet's orbital angular momentum per unit mass to evolve in time as
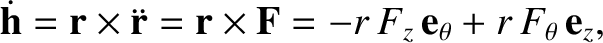 |
(I.18) |
where Equations (I.2), (I.6), (I.14), and (I.15) have been employed.
Consequently,
Furthermore,
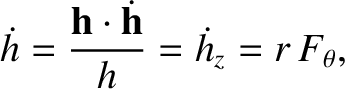 |
(I.22) |
where use has been made of Equation (I.6).
The perturbing force causes the planet's eccentricity vector to evolve in time as
where Equations (I.7), (I.8), (I.14), (I.15), and (I.18) have been employed.
It follows that
where use has been made of Equation (I.11).
Furthermore,
![$\displaystyle \skew{3}\dot{e} = \frac{{\bf e}\cdot\dot{\bf e}}{e} = \skew{3}\do...
..._x = \frac{h}{\mu}\left[ \sin\theta\,F_r+(\cos\theta+\cos E)\,F_\theta \right],$](img5113.png) |
(I.27) |
where Equation (I.8) has been employed.
Differentiation of Equation (I.9) with respect to time yields
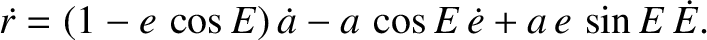 |
(I.28) |
Making use of Equations (I.4), (I.7), and (I.10), we can rearrange the previous expression to give
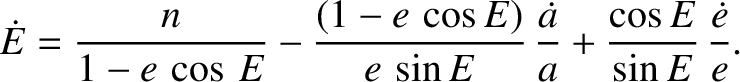 |
(I.29) |
Differentiation of Equation (I.13) with respect to time yields
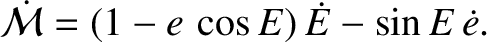 |
(I.30) |
The previous two equations can be combined to give
where use has been made of Equations (I.9), (I.11), and (I.12). Thus, it follows from Equations (I.11), (I.17), and
(I.27) that
![$\displaystyle \skew{5}\dot{\cal M} = n + \frac{h}{\mu}\,\frac{(1-e^{\,2})^{1/2}...
... -\left[1+\frac{1}{(1-e^{\,2})}\,\frac{r}{a}\right]\sin\theta\,F_\theta\right).$](img5120.png) |
(I.32) |
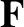 . Consequently, the planet's perturbed equation of motion becomes
We can write
. Consequently, the planet's perturbed equation of motion becomes
We can write
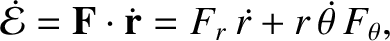
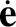
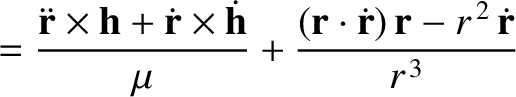
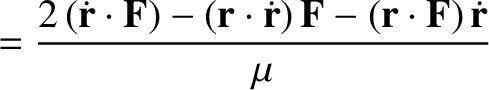
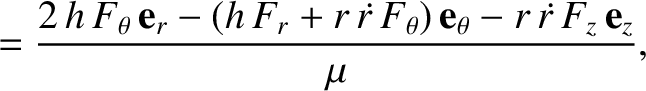
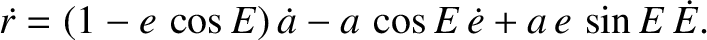
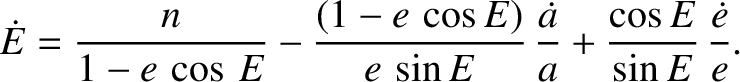
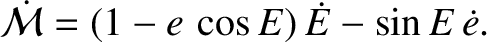
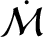
![$\displaystyle = n + \frac{1}{e\,\sin E}\left[(\cos E - e)\,\skew{3}\dot{e} - \left(\frac{r}{a}\right)^2\,\frac{\skew{3}\dot{a}}{a}\right]$](img5118.png)
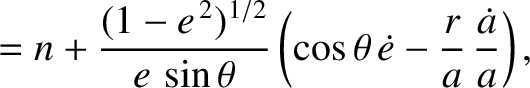
![$\displaystyle \skew{5}\dot{\cal M} = n + \frac{h}{\mu}\,\frac{(1-e^{\,2})^{1/2}...
... -\left[1+\frac{1}{(1-e^{\,2})}\,\frac{r}{a}\right]\sin\theta\,F_\theta\right).$](img5120.png)