Next: Perturbed planetary orbit Up: Derivation of Gauss planetary Previous: Derivation of Gauss planetary
 and relative position vector
and relative position vector  that is orbiting around the Sun, whose mass is
that is orbiting around the Sun, whose mass is  . The planet's unperturbed equation of motion is written (see Section 4.16)
. The planet's unperturbed equation of motion is written (see Section 4.16)
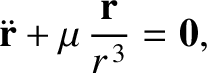 |
(I.1) |
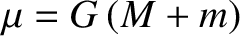 . As described in Chapter 4, the solution to this equation is
a Keplerian ellipse.
. As described in Chapter 4, the solution to this equation is
a Keplerian ellipse.
Let  ,
,  ,
,  be a Cartesian coordinate system in a reference frame whose origin corresponds to the location of the Sun,
and which is such that the planet's unperturbed orbit lies in the plane
be a Cartesian coordinate system in a reference frame whose origin corresponds to the location of the Sun,
and which is such that the planet's unperturbed orbit lies in the plane  , with the
angular momentum vector pointing in the positive
, with the
angular momentum vector pointing in the positive  -direction, and the perihelion situated on the positive
-direction, and the perihelion situated on the positive  -axis.
Let
-axis.
Let  ,
,  ,
,  be a cylindrical coordinate system in the same reference frame.
be a cylindrical coordinate system in the same reference frame.
We know from the analysis of Chapter 4 that
where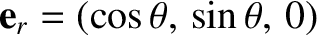 and
and
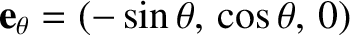 .
Moreover, the planet's mean orbital angular velocity is
its orbital energy per unit mass is
its orbital angular momentum per unit mass is
where
and its eccentricity vector is
Here,
.
Moreover, the planet's mean orbital angular velocity is
its orbital energy per unit mass is
its orbital angular momentum per unit mass is
where
and its eccentricity vector is
Here,  and
and  are the planet's orbital major radius and eccentricity, respectively.
Note that, for the unperturbed orbit, the quantities
are the planet's orbital major radius and eccentricity, respectively.
Note that, for the unperturbed orbit, the quantities  ,
,  ,
,  ,
,  ,
, 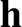 , and
, and 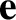 are all constant in time.
We also have
where
are all constant in time.
We also have
where  ,
,  , and
, and 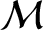 are the planet's true anomaly, eccentric anomaly, and mean anomaly,
respectively. (See Chapter 4.)
are the planet's true anomaly, eccentric anomaly, and mean anomaly,
respectively. (See Chapter 4.)