Stability of Lagrange points
We have seen that the five Lagrange points, 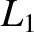 to
to  , are the equilibrium points
of mass
, are the equilibrium points
of mass  in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
The equations of motion of mass  in the co-rotating frame are
specified in Equations (9.27)–(9.29). Note that the motion
in the
in the co-rotating frame are
specified in Equations (9.27)–(9.29). Note that the motion
in the  -
- plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the
plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the  -axis simply
corresponds to motion in the potential
-axis simply
corresponds to motion in the potential 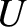 . Hence, the condition for
the stability of the Lagrange points (which all lie at
. Hence, the condition for
the stability of the Lagrange points (which all lie at  ) to small displacements parallel
to the
) to small displacements parallel
to the  -axis is simply (see Section 2.7)
-axis is simply (see Section 2.7)
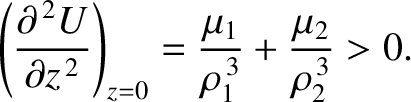 |
(9.67) |
This condition is satisfied everywhere in the  -
- plane. Hence, the Lagrange points are all
stable to small displacements parallel to the
plane. Hence, the Lagrange points are all
stable to small displacements parallel to the  -axis. It thus remains to investigate
their stability to small displacements lying within the
-axis. It thus remains to investigate
their stability to small displacements lying within the  -
- plane.
plane.
Suppose that a Lagrange point is situated in the  -
- plane at coordinates
plane at coordinates
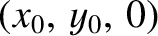 .
Let us consider small amplitude
.
Let us consider small amplitude  -
- motion in the vicinity of this point by writing
motion in the vicinity of this point by writing
where  and
and 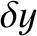 are infinitesimal. Expanding
are infinitesimal. Expanding 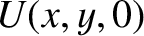 about the Lagrange point as a Taylor series, and retaining terms up to second order in small
quantities, we obtain
about the Lagrange point as a Taylor series, and retaining terms up to second order in small
quantities, we obtain
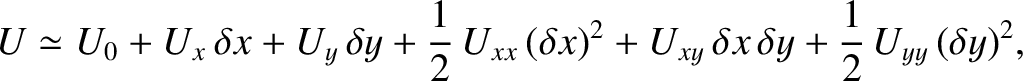 |
(9.71) |
where
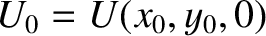 ,
,
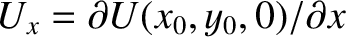 ,
,
 ,
and so on. However, by definition,
,
and so on. However, by definition,  at a Lagrange point, so the expansion simplifies to
at a Lagrange point, so the expansion simplifies to
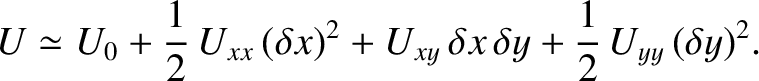 |
(9.72) |
Finally, substituting Equations (9.68)–(9.70), and (9.72)
into the equations of  -
- motion, (9.27) and (9.28), and only retaining terms up to
first order in small quantities, we get
as
motion, (9.27) and (9.28), and only retaining terms up to
first order in small quantities, we get
as
 .
.
Let us search for a solution of the preceding pair of equations
of the form
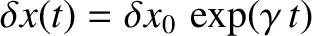 and
and
 . We obtain
. We obtain
![\begin{displaymath}\left(
\begin{array}{cc}
\gamma^{\,2} + U_{xx},& -2\,\gamma+U...
...ht) = \left(
\begin{array}{c}
0\\ [0.5ex]
0
\end{array}\right).\end{displaymath}](img2267.png) |
(9.75) |
This equation only has a nontrivial solution if the determinant of the
matrix is zero. Hence, we get
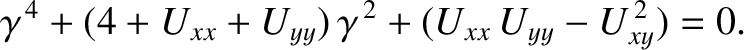 |
(9.76) |
It is convenient to define
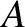 |
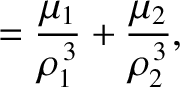 |
(9.77) |
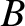 |
![$\displaystyle = 3\left[ \frac{\mu_1}{\rho_1^{\,5}} + \frac{\mu_2}{\rho_2^{\,5}}\right]y^{\,2},$](img2272.png) |
(9.78) |
 |
![$\displaystyle = 3\left[\frac{\mu_1\,(x+\mu_2)}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)}{\rho_2^{\,5}}\right]y,$](img2274.png) |
(9.79) |
 |
![$\displaystyle = 3\left[\frac{\mu_1\,(x+\mu_2)^2}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)^2}{\rho_2^{\,5}}\right],$](img2276.png) |
(9.80) |
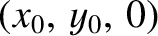 . It thus follows that
. It thus follows that
Figure: 9.13
The solid, dashed, and dotted curves show  as a function of
as a function of 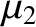 at
at
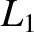 ,
, 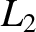 , and
, and 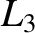 Lagrange points, respectively.
Lagrange points, respectively.
|
|
Consider the co-linear Lagrange points, 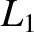 ,
, 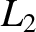 , and
, and 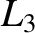 . These all
lie on the
. These all
lie on the  -axis, and are thus characterized by
-axis, and are thus characterized by
 ,
,
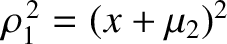 , and
, and
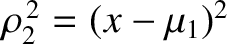 . It follows,
from the preceding equations, that
. It follows,
from the preceding equations, that  and
and 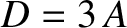 . Hence,
. Hence,
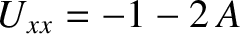 ,
,
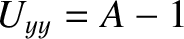 , and
, and 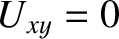 . Equation (9.76) thus yields
. Equation (9.76) thus yields
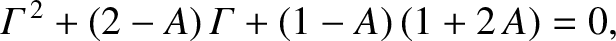 |
(9.84) |
where
 . For a Lagrange point to be stable
to small displacements, all four of the roots,
. For a Lagrange point to be stable
to small displacements, all four of the roots,  , of Equation (9.76) must
be purely imaginary. This, in turn, implies that the two roots of
the preceding equation,
, of Equation (9.76) must
be purely imaginary. This, in turn, implies that the two roots of
the preceding equation,
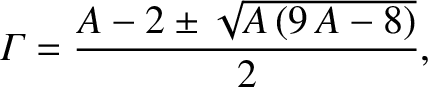 |
(9.85) |
must both be real and negative.
Thus, the stability criterion is
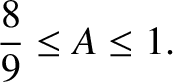 |
(9.86) |
Figure 9.13 shows  calculated at the three co-linear Lagrange points as a function of
calculated at the three co-linear Lagrange points as a function of 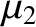 , for all
allowed values of this parameter (i.e.,
, for all
allowed values of this parameter (i.e.,
 ). It can be seen that
). It can be seen that  is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points,
is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points, 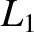 ,
, 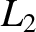 , and
, and 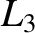 , are intrinsically unstable equilibrium points in the co-rotating
frame.
, are intrinsically unstable equilibrium points in the co-rotating
frame.
Figure: 9.14
Positions of the Trojan asteroids (small circles) and Jupiter (large circle) projected
onto ecliptic plane (viewed from north) at MJD 55600. The  -axis is directed toward
vernal equinox. Raw data from JPL Small-Body Database.
-axis is directed toward
vernal equinox. Raw data from JPL Small-Body Database.
|
|
Let us now consider the triangular Lagrange points, 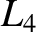 and
and  . These points
are characterized by
. These points
are characterized by
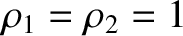 . It follows that
. It follows that 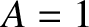 ,
, 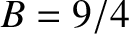 ,
,
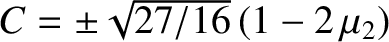 ,
and
,
and 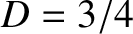 . Hence,
. Hence,
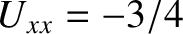 ,
,
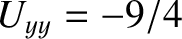 , and
, and
 ,
where the upper and lower signs corresponds to
,
where the upper and lower signs corresponds to 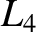 and
and  , respectively.
Equation (9.76) thus yields
, respectively.
Equation (9.76) thus yields
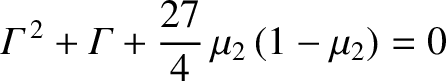 |
(9.87) |
for both points,
where
 . As before, the stability criterion is that the two roots of the
preceding equation must both be
real and negative. This is the case provided that
. As before, the stability criterion is that the two roots of the
preceding equation must both be
real and negative. This is the case provided that
 , which
yields the stability criterion
, which
yields the stability criterion
 |
(9.88) |
In unnormalized units, this criterion becomes
 |
(9.89) |
Figure: 9.15
Positions of the Trojan asteroids (small circles) and Jupiter (large circle) at MJD 55600.  is normal distance from the ecliptic plane.
is normal distance from the ecliptic plane.
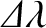 is the difference in
ecliptic longitude between the asteroids and Jupiter. Raw data from JPL Small-Body Database.
is the difference in
ecliptic longitude between the asteroids and Jupiter. Raw data from JPL Small-Body Database.
|
|
We thus conclude that the 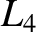 and
and  Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass
Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass 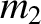 is less than about
is less than about 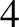 percent of
mass
percent of
mass  . If this is the case then mass
. If this is the case then mass  can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass
can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass 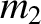 about mass
about mass  , but it will stay approximately
, but it will stay approximately 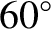 ahead of
mass
ahead of
mass 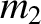 if it is orbiting the
if it is orbiting the 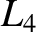 point, or
point, or 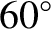 behind if it is orbiting the
behind if it is orbiting the  point. See Figure 9.12. This type of behavior has been observed in the solar system. For instance,
there is a subclass of asteroids, known as the Trojan asteroids, that are trapped
in the vicinity of the
point. See Figure 9.12. This type of behavior has been observed in the solar system. For instance,
there is a subclass of asteroids, known as the Trojan asteroids, that are trapped
in the vicinity of the 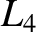 and
and  points of the Sun-Jupiter system [which easily
satisfies the stability criterion in Equation (9.89)], and consequently share Jupiter's orbit around the Sun,
staying approximately
points of the Sun-Jupiter system [which easily
satisfies the stability criterion in Equation (9.89)], and consequently share Jupiter's orbit around the Sun,
staying approximately 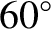 ahead of and
ahead of and 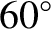 behind, Jupiter, respectively. These asteroids
are shown in Figures 9.14 and 9.15. The Sun-Jupiter system is not the only dynamical system in the solar system that possess
Trojan asteroids trapped in the vicinity of its
behind, Jupiter, respectively. These asteroids
are shown in Figures 9.14 and 9.15. The Sun-Jupiter system is not the only dynamical system in the solar system that possess
Trojan asteroids trapped in the vicinity of its 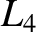 and
and  points. In fact, the Sun-Neptune system has eight known Trojan asteroids,
the Sun-Mars system has four, and the Sun-Earth system has one (designated 2010 TK7) trapped at the
points. In fact, the Sun-Neptune system has eight known Trojan asteroids,
the Sun-Mars system has four, and the Sun-Earth system has one (designated 2010 TK7) trapped at the 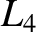 point.
The
point.
The 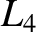 and
and  points of the Sun-Earth system are also observed to trap clouds of interplanetary dust.
points of the Sun-Earth system are also observed to trap clouds of interplanetary dust.
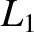 to
to  , are the equilibrium points
of mass
, are the equilibrium points
of mass  in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
in the co-rotating frame. Let us now determine whether or not
these equilibrium points are stable to small displacements.
 in the co-rotating frame are
specified in Equations (9.27)–(9.29). Note that the motion
in the
in the co-rotating frame are
specified in Equations (9.27)–(9.29). Note that the motion
in the  -
- plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the
plane is complicated by presence of the Coriolis acceleration. However, the motion parallel to the  -axis simply
corresponds to motion in the potential
-axis simply
corresponds to motion in the potential 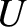 . Hence, the condition for
the stability of the Lagrange points (which all lie at
. Hence, the condition for
the stability of the Lagrange points (which all lie at  ) to small displacements parallel
to the
) to small displacements parallel
to the  -axis is simply (see Section 2.7)
-axis is simply (see Section 2.7)
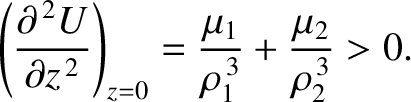
 -
- plane. Hence, the Lagrange points are all
stable to small displacements parallel to the
plane. Hence, the Lagrange points are all
stable to small displacements parallel to the  -axis. It thus remains to investigate
their stability to small displacements lying within the
-axis. It thus remains to investigate
their stability to small displacements lying within the  -
- plane.
plane.
 -
- plane at coordinates
plane at coordinates
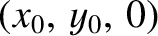 .
Let us consider small amplitude
.
Let us consider small amplitude  -
- motion in the vicinity of this point by writing
motion in the vicinity of this point by writing
 and
and 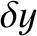 are infinitesimal. Expanding
are infinitesimal. Expanding 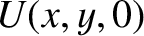 about the Lagrange point as a Taylor series, and retaining terms up to second order in small
quantities, we obtain
about the Lagrange point as a Taylor series, and retaining terms up to second order in small
quantities, we obtain
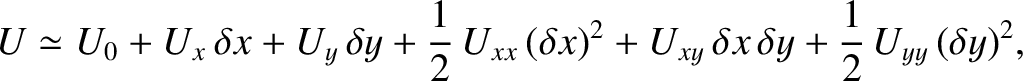
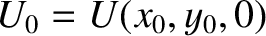 ,
,
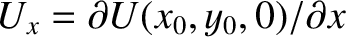 ,
,
 ,
and so on. However, by definition,
,
and so on. However, by definition,  at a Lagrange point, so the expansion simplifies to
Finally, substituting Equations (9.68)–(9.70), and (9.72)
into the equations of
at a Lagrange point, so the expansion simplifies to
Finally, substituting Equations (9.68)–(9.70), and (9.72)
into the equations of  -
- motion, (9.27) and (9.28), and only retaining terms up to
first order in small quantities, we get
motion, (9.27) and (9.28), and only retaining terms up to
first order in small quantities, we get

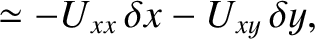
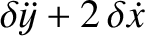
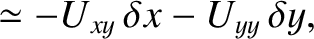
 .
.
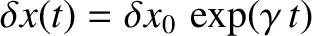 and
and
 . We obtain
. We obtain
![\begin{displaymath}\left(
\begin{array}{cc}
\gamma^{\,2} + U_{xx},& -2\,\gamma+U...
...ht) = \left(
\begin{array}{c}
0\\ [0.5ex]
0
\end{array}\right).\end{displaymath}](img2267.png)
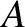
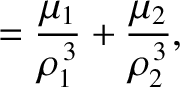
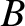
![$\displaystyle = 3\left[ \frac{\mu_1}{\rho_1^{\,5}} + \frac{\mu_2}{\rho_2^{\,5}}\right]y^{\,2},$](img2272.png)

![$\displaystyle = 3\left[\frac{\mu_1\,(x+\mu_2)}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)}{\rho_2^{\,5}}\right]y,$](img2274.png)
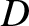
![$\displaystyle = 3\left[\frac{\mu_1\,(x+\mu_2)^2}{\rho_1^{\,5}}+\frac{\mu_2\,(x-\mu_1)^2}{\rho_2^{\,5}}\right],$](img2276.png)
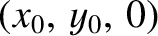 . It thus follows that
. It thus follows that
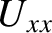
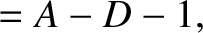
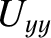
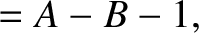
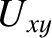
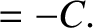
![\includegraphics[height=3.5in]{Chapter08/fig8_13.eps}](img2283.png)
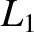 ,
, 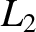 , and
, and 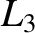 . These all
lie on the
. These all
lie on the  -axis, and are thus characterized by
-axis, and are thus characterized by
 ,
,
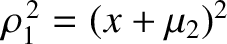 , and
, and
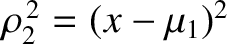 . It follows,
from the preceding equations, that
. It follows,
from the preceding equations, that  and
and 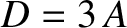 . Hence,
. Hence,
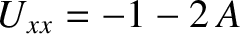 ,
,
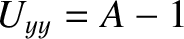 , and
, and 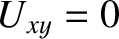 . Equation (9.76) thus yields
. Equation (9.76) thus yields
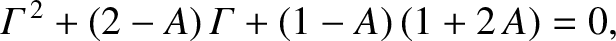
 . For a Lagrange point to be stable
to small displacements, all four of the roots,
. For a Lagrange point to be stable
to small displacements, all four of the roots,  , of Equation (9.76) must
be purely imaginary. This, in turn, implies that the two roots of
the preceding equation,
, of Equation (9.76) must
be purely imaginary. This, in turn, implies that the two roots of
the preceding equation,
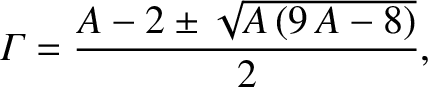
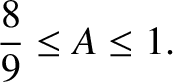
 calculated at the three co-linear Lagrange points as a function of
calculated at the three co-linear Lagrange points as a function of  , for all
allowed values of this parameter (i.e.,
, for all
allowed values of this parameter (i.e.,
 ). It can be seen that
). It can be seen that  is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points,
is always greater than unity for all three points. Hence, we conclude that the co-linear
Lagrange points, 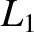 ,
, 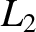 , and
, and 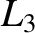 , are intrinsically unstable equilibrium points in the co-rotating
frame.
, are intrinsically unstable equilibrium points in the co-rotating
frame.
![\includegraphics[height=4in]{Chapter08/fig8_14.eps}](img2296.png)
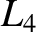 and
and  . These points
are characterized by
. These points
are characterized by
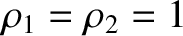 . It follows that
. It follows that 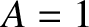 ,
, 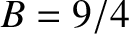 ,
,
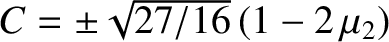 ,
and
,
and 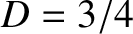 . Hence,
. Hence,
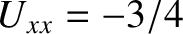 ,
,
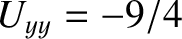 , and
, and
 ,
where the upper and lower signs corresponds to
,
where the upper and lower signs corresponds to 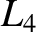 and
and  , respectively.
Equation (9.76) thus yields
, respectively.
Equation (9.76) thus yields
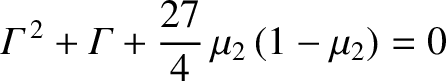
 . As before, the stability criterion is that the two roots of the
preceding equation must both be
real and negative. This is the case provided that
. As before, the stability criterion is that the two roots of the
preceding equation must both be
real and negative. This is the case provided that
 , which
yields the stability criterion
, which
yields the stability criterion

![\includegraphics[height=4in]{Chapter08/fig8_15.eps}](img2309.png)
 and
and  Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass
Lagrange points are stable equilibrium
points, in the co-rotating frame, provided that mass 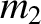 is less than about
is less than about  percent of
mass
percent of
mass  . If this is the case then mass
. If this is the case then mass  can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass
can orbit around these points
indefinitely. In the inertial frame, the mass will share
the orbit of mass 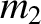 about mass
about mass  , but it will stay approximately
, but it will stay approximately 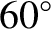 ahead of
mass
ahead of
mass 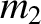 if it is orbiting the
if it is orbiting the 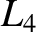 point, or
point, or 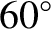 behind if it is orbiting the
behind if it is orbiting the  point. See Figure 9.12. This type of behavior has been observed in the solar system. For instance,
there is a subclass of asteroids, known as the Trojan asteroids, that are trapped
in the vicinity of the
point. See Figure 9.12. This type of behavior has been observed in the solar system. For instance,
there is a subclass of asteroids, known as the Trojan asteroids, that are trapped
in the vicinity of the 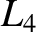 and
and  points of the Sun-Jupiter system [which easily
satisfies the stability criterion in Equation (9.89)], and consequently share Jupiter's orbit around the Sun,
staying approximately
points of the Sun-Jupiter system [which easily
satisfies the stability criterion in Equation (9.89)], and consequently share Jupiter's orbit around the Sun,
staying approximately 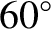 ahead of and
ahead of and 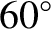 behind, Jupiter, respectively. These asteroids
are shown in Figures 9.14 and 9.15. The Sun-Jupiter system is not the only dynamical system in the solar system that possess
Trojan asteroids trapped in the vicinity of its
behind, Jupiter, respectively. These asteroids
are shown in Figures 9.14 and 9.15. The Sun-Jupiter system is not the only dynamical system in the solar system that possess
Trojan asteroids trapped in the vicinity of its  and
and  points. In fact, the Sun-Neptune system has eight known Trojan asteroids,
the Sun-Mars system has four, and the Sun-Earth system has one (designated 2010 TK7) trapped at the
points. In fact, the Sun-Neptune system has eight known Trojan asteroids,
the Sun-Mars system has four, and the Sun-Earth system has one (designated 2010 TK7) trapped at the  point.
The
point.
The  and
and  points of the Sun-Earth system are also observed to trap clouds of interplanetary dust.
points of the Sun-Earth system are also observed to trap clouds of interplanetary dust.