Lagrange planetary equations
Now,
with
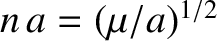 .
Hence,
.
Hence,
 |
 |
(G.89) |
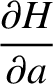 |
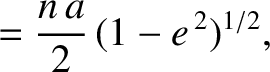 |
(G.90) |
 |
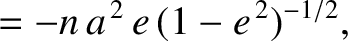 |
(G.91) |
 |
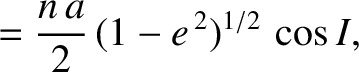 |
(G.92) |
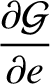 |
 |
(G.93) |
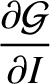 |
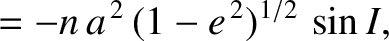 |
(G.94) |
![$\displaystyle [\skew{5}\bar{\lambda}_0,a] =-[a,\skew{5}\bar{\lambda}_0]$](img4813.png) |
 |
(G.95) |
![$\displaystyle [\varpi,a]=-[a,\varpi]$](img4814.png) |
![$\displaystyle = - \frac{n\,a}{2}\,[1-(1-e^{\,2})^{1/2}],$](img4815.png) |
(G.96) |
![$\displaystyle [{\mit\Omega},a]=-[a,{\mit\Omega}]$](img4816.png) |
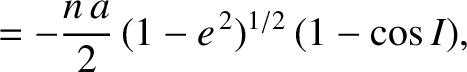 |
(G.97) |
![$\displaystyle [\varpi,e] = -[e,\varpi]$](img4818.png) |
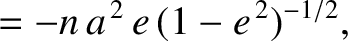 |
(G.98) |
![$\displaystyle [{\mit\Omega},e]=-[e,{\mit\Omega}]$](img4819.png) |
 |
(G.99) |
![$\displaystyle [{\mit\Omega}, I]=-[I,{\mit\Omega}]$](img4821.png) |
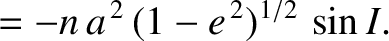 |
(G.100) |
![$\displaystyle [a,\skew{5}\bar{\lambda}_0]\,\frac{d \skew{5}\bar{\lambda}_0}{ dt} + [a,\varpi]\,\frac{d\varpi}{d t} + [a,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4823.png) |
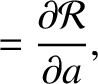 |
(G.101) |
![$\displaystyle [e,\varpi]\,\frac{d\varpi}{d t} + [e,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4825.png) |
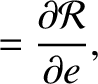 |
(G.102) |
![$\displaystyle [\skew{5}\bar{\lambda}_0,a]\,\frac{d a}{d t}$](img4827.png) |
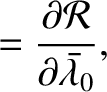 |
(G.103) |
![$\displaystyle [I,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4829.png) |
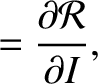 |
(G.104) |
![$\displaystyle [{\mit\Omega},a]\,\frac{d a}{d t} + [{\mit\Omega},e]\,\frac{d e}{d t} + [{\mit\Omega}, I]\,\frac{d I}{d t}$](img4831.png) |
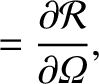 |
(G.105) |
![$\displaystyle [\varpi,a]\,\frac{d a}{d t} + [\varpi,e]\,\frac{d e}{d t}$](img4833.png) |
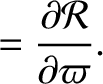 |
(G.106) |
In fact, the orbital element
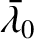 always appears in the disturbing function in the
combination
always appears in the disturbing function in the
combination
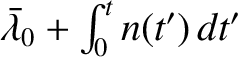 . This combination is known as the mean longitude, and is
denote
. This combination is known as the mean longitude, and is
denote
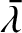 . It follows that
. It follows that
The integral appearing in the previous equation is problematic.
Fortunately, it can easily be eliminated by replacing the variable
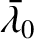 by
by
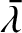 . In this case, the Lagrange planetary equations become
where
. In this case, the Lagrange planetary equations become
where
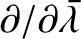 is taken at
constant
is taken at
constant  , and
, and
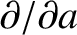 at constant
at constant
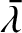 (Brouwer and Clemence 1961).
(Brouwer and Clemence 1961).
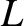
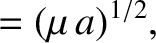
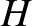
![$\displaystyle = [\mu\,a\,(1-e^{\,2})]^{1/2},$](img4797.png)

![$\displaystyle = [\mu\,a\,(1-e^{\,2})]^{1/2}\,\cos I,$](img4799.png)
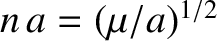 .
Hence,
.
Hence,


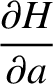
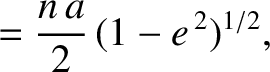

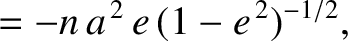

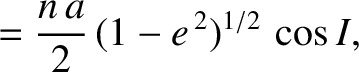
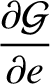

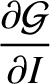
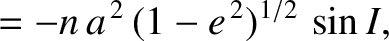
![$\displaystyle [\skew{5}\bar{\lambda}_0,a] =-[a,\skew{5}\bar{\lambda}_0]$](img4813.png)

![$\displaystyle [\varpi,a]=-[a,\varpi]$](img4814.png)
![$\displaystyle = - \frac{n\,a}{2}\,[1-(1-e^{\,2})^{1/2}],$](img4815.png)
![$\displaystyle [{\mit\Omega},a]=-[a,{\mit\Omega}]$](img4816.png)
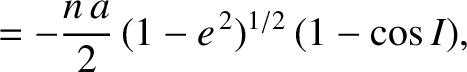
![$\displaystyle [\varpi,e] = -[e,\varpi]$](img4818.png)
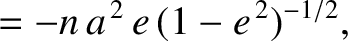
![$\displaystyle [{\mit\Omega},e]=-[e,{\mit\Omega}]$](img4819.png)

![$\displaystyle [{\mit\Omega}, I]=-[I,{\mit\Omega}]$](img4821.png)
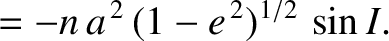
![$\displaystyle [a,\skew{5}\bar{\lambda}_0]\,\frac{d \skew{5}\bar{\lambda}_0}{ dt} + [a,\varpi]\,\frac{d\varpi}{d t} + [a,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4823.png)
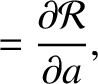
![$\displaystyle [e,\varpi]\,\frac{d\varpi}{d t} + [e,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4825.png)
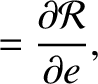
![$\displaystyle [\skew{5}\bar{\lambda}_0,a]\,\frac{d a}{d t}$](img4827.png)
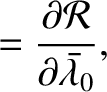
![$\displaystyle [I,{\mit\Omega}]\,\frac{d{\mit\Omega}}{d t}$](img4829.png)
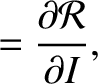
![$\displaystyle [{\mit\Omega},a]\,\frac{d a}{d t} + [{\mit\Omega},e]\,\frac{d e}{d t} + [{\mit\Omega}, I]\,\frac{d I}{d t}$](img4831.png)
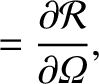
![$\displaystyle [\varpi,a]\,\frac{d a}{d t} + [\varpi,e]\,\frac{d e}{d t}$](img4833.png)
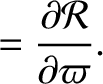
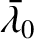 always appears in the disturbing function in the
combination
always appears in the disturbing function in the
combination
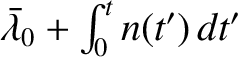 . This combination is known as the mean longitude, and is
denote
. This combination is known as the mean longitude, and is
denote
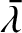 . It follows that
. It follows that
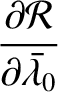
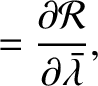
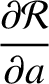
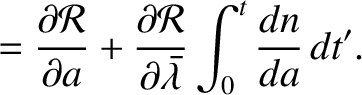
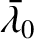 by
by
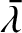 . In this case, the Lagrange planetary equations become
where
. In this case, the Lagrange planetary equations become
where
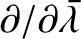 is taken at
constant
is taken at
constant  , and
, and
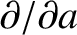 at constant
at constant
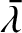 (Brouwer and Clemence 1961).
(Brouwer and Clemence 1961).