Six new equations can be derived from Equations (G.24)–(G.29)
by multiplying them successively by
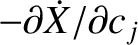 ,
,
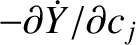 ,
,
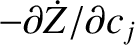 ,
,
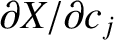 ,
,
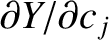 , and
, and
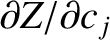 , and then
summing the resulting equations. The right-hand sides
of the new equations are
, and then
summing the resulting equations. The right-hand sides
of the new equations are
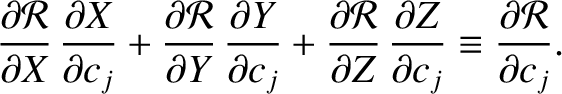 |
(G.30) |
The new equations can be written in a more compact form via
the introduction of Lagrange brackets, which are defined as
![$\displaystyle [c_j,c_k] \equiv \sum_{l=1,3}\left(\frac{\partial X_l}{\partial c...
...ac{\partial X_l}{\partial c_k}\,\frac{\partial \dot{X}_l}{\partial c_j}\right),$](img4685.png) |
(G.31) |
where
 ,
,
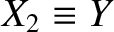 , and
, and
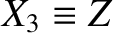 .
Thus, the new equations become
.
Thus, the new equations become
![$\displaystyle \sum_{k=1,6}[c_j, c_k]\,\frac{dc_k}{dt} = \frac{\partial {\cal R}}{\partial c_j},$](img4689.png) |
(G.32) |
for  .
Note, incidentally, that
.
Note, incidentally, that
Let
![$\displaystyle [p,q] = \sum_{l=1,3}\left(\frac{\partial X_l}{\partial p}\,\frac{...
... \frac{\partial X_l}{\partial q}\,\frac{\partial \dot{X}_l}{\partial p}\right),$](img4694.png) |
(G.35) |
where 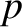 and
and  are any two orbital elements. It follows that
are any two orbital elements. It follows that
![$\displaystyle \frac{\partial}{\partial t} [p,q] = \sum_{l=1,3}\left(\frac{\part...
...l}{\partial q}\,\frac{\partial^{\,2} \dot{X}_l}{\partial p\,\partial t}\right),$](img4695.png) |
(G.36) |
or
![$\displaystyle \frac{\partial}{\partial t} [p,q]= \sum_{l=1,3}\left[
\frac{\part...
...\partial X_l}{\partial p}\,\frac{\partial \dot{X}_l}{\partial t}\right)\right].$](img4696.png) |
(G.37) |
However, in the preceding expression, 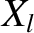 and
and 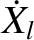 stand for
coordinates and velocities of Keplerian orbits calculated with
stand for
coordinates and velocities of Keplerian orbits calculated with
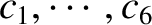 treated as constants. Thus, we can write
treated as constants. Thus, we can write
 and
and
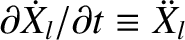 , giving
, giving
![$\displaystyle \frac{\partial}{\partial t} [p,q]= \sum_{l=1,3}\left[
\frac{\part...
...rac{\partial F_0}{\partial X_l}\,\frac{\partial X_l}{\partial p}\right)\right],$](img4701.png) |
(G.38) |
because
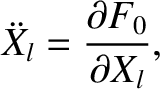 |
(G.39) |
where
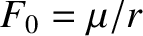 .
Expression (G.38) reduces to
.
Expression (G.38) reduces to
![$\displaystyle \frac{\partial}{\partial t}[p,q] = \frac{1}{2}\frac{\partial^{\,2...
...partial q\,\partial p} + \frac{\partial^{\,2} F_0}{\partial q\,\partial p} = 0,$](img4704.png) |
(G.40) |
where
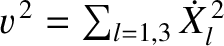 . Hence, we conclude that
Lagrange brackets are functions of the osculating orbital
elements,
. Hence, we conclude that
Lagrange brackets are functions of the osculating orbital
elements,
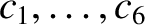 , but are not explicit functions of
, but are not explicit functions of 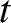 .
It follows that we can evaluate these brackets at any convenient point in the orbit.
.
It follows that we can evaluate these brackets at any convenient point in the orbit.
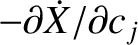 ,
,
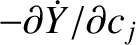 ,
,
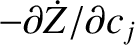 ,
,
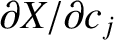 ,
,
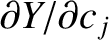 , and
, and
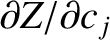 , and then
summing the resulting equations. The right-hand sides
of the new equations are
, and then
summing the resulting equations. The right-hand sides
of the new equations are
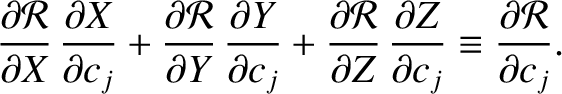
![$\displaystyle [c_j,c_k] \equiv \sum_{l=1,3}\left(\frac{\partial X_l}{\partial c...
...ac{\partial X_l}{\partial c_k}\,\frac{\partial \dot{X}_l}{\partial c_j}\right),$](img4685.png)
 ,
,
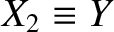 , and
, and
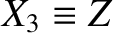 .
Thus, the new equations become
for
.
Thus, the new equations become
for  .
Note, incidentally, that
.
Note, incidentally, that
![$\displaystyle [c_j,c_j]$](img4691.png)
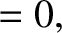
![$\displaystyle [c_j,c_k]$](img4692.png)
![$\displaystyle = -[c_k,c_j].$](img4693.png)
![$\displaystyle [p,q] = \sum_{l=1,3}\left(\frac{\partial X_l}{\partial p}\,\frac{...
... \frac{\partial X_l}{\partial q}\,\frac{\partial \dot{X}_l}{\partial p}\right),$](img4694.png)
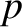 and
and  are any two orbital elements. It follows that
are any two orbital elements. It follows that
![$\displaystyle \frac{\partial}{\partial t} [p,q] = \sum_{l=1,3}\left(\frac{\part...
...l}{\partial q}\,\frac{\partial^{\,2} \dot{X}_l}{\partial p\,\partial t}\right),$](img4695.png)
![$\displaystyle \frac{\partial}{\partial t} [p,q]= \sum_{l=1,3}\left[
\frac{\part...
...\partial X_l}{\partial p}\,\frac{\partial \dot{X}_l}{\partial t}\right)\right].$](img4696.png)
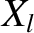 and
and 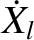 stand for
coordinates and velocities of Keplerian orbits calculated with
stand for
coordinates and velocities of Keplerian orbits calculated with
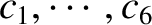 treated as constants. Thus, we can write
treated as constants. Thus, we can write
 and
and
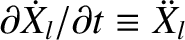 , giving
because
, giving
because
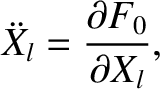
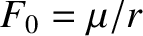 .
Expression (G.38) reduces to
.
Expression (G.38) reduces to
![$\displaystyle \frac{\partial}{\partial t}[p,q] = \frac{1}{2}\frac{\partial^{\,2...
...partial q\,\partial p} + \frac{\partial^{\,2} F_0}{\partial q\,\partial p} = 0,$](img4704.png)
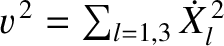 . Hence, we conclude that
Lagrange brackets are functions of the osculating orbital
elements,
. Hence, we conclude that
Lagrange brackets are functions of the osculating orbital
elements,
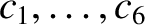 , but are not explicit functions of
, but are not explicit functions of 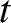 .
It follows that we can evaluate these brackets at any convenient point in the orbit.
.
It follows that we can evaluate these brackets at any convenient point in the orbit.