Regression of lunar ascending node

According to Equations (11.207) and (11.314), the mean ecliptic longitude of the lunar ascending node evolves in time as

$$\gamma = \gamma_0 - \gamma'\,n'\,t,$$ (11.339)

where

$$\gamma' = g\,m = \frac{3}{4}\,m - \frac{9}{32}\,m^{\,2} + {\cal O}(m^{\,3}).$$ (11.340)

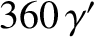Equation (11.339) implies that the ascending node regresses (i.e., its longitude decreases in time) at the mean rate of $360\,\gamma'$ degrees per year. As before, it is clear that this regression is entirely due to the perturbing influence of the Sun. Moreover, we find that the ascending node retreats by 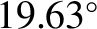$19.63^\circ$ degrees per year. Hence, we predict that the ascending node completes a full circuit about the Earth every 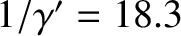$1/\gamma'=18.3$ years. 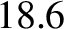In fact, the lunar ascending node completes a full circuit every $18.6$ years, so our prediction is fairly accurate.