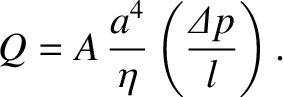Consider a viscous fluid flowing through a circular pipe. The volume rate of
fluid flow through the pipe, 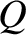 , might plausibly depend on the radius of the pipe,
, might plausibly depend on the radius of the pipe, 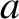 , the viscosity of the
fluid,
, the viscosity of the
fluid, 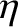 , and the pressure gradient along the pipe,
, and the pressure gradient along the pipe,
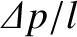 . Here,
. Here,
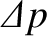 is the pressure
difference between the two ends of the pipe, and
is the pressure
difference between the two ends of the pipe, and  is the length of the pipe.
Let us guess that
is the length of the pipe.
Let us guess that
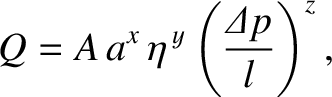 |
(1.5) |
where  ,
,  , and
, and  are, as yet, unknown exponents, and
are, as yet, unknown exponents, and  is a dimensionless constant.
Now, the dimensions of
is a dimensionless constant.
Now, the dimensions of 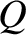 are
are ![$[L]^3/[T]$](img122.png) , the dimensions of
, the dimensions of 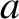 are
are ![$[L]$](img123.png) , the dimensions
of
, the dimensions
of 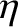 are
are
![$[M]/([L]\,[T])$](img124.png) , and the dimensions of
, and the dimensions of
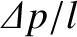 are
are
![$\{([M]\,[L]/[T]^2)/[L]^2\}/[L] = [M]/([L]^2\,[T]^2)$](img125.png) .
Thus, equating the dimensions of the left- and right-hand sides of the previous equation, we obtain
.
Thus, equating the dimensions of the left- and right-hand sides of the previous equation, we obtain
![$\displaystyle \frac{[L]^3}{[T]} = [L]^x\left(\frac{[M]}{[L]\,[T]}\right)^y\left(\frac{[M]}{[L]^2\,[T]^2}\right)^z.$](img126.png) |
(1.6) |
Now, if Equation (1.5) is to be dimensionally consistent then we can separately equate the
exponents of length, mass, and time in the previous expression. Equating the exponents of ![$[L]$](img123.png) ,
we obtain
,
we obtain
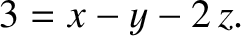 |
(1.7) |
Equating the exponents of ![$[M]$](img128.png) , we get
, we get
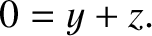 |
(1.8) |
Finally, equating the exponents of ![$[T]$](img130.png) , we obtain
, we obtain
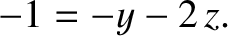 |
(1.9) |
It is easily seen that  ,
,  , and
, and 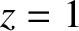 . Hence, we deduce that
. Hence, we deduce that
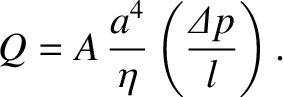 |
(1.10) |
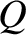 , might plausibly depend on the radius of the pipe,
, might plausibly depend on the radius of the pipe, 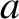 , the viscosity of the
fluid,
, the viscosity of the
fluid, 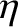 , and the pressure gradient along the pipe,
, and the pressure gradient along the pipe,
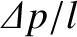 . Here,
. Here,
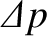 is the pressure
difference between the two ends of the pipe, and
is the pressure
difference between the two ends of the pipe, and  is the length of the pipe.
Let us guess that
where
is the length of the pipe.
Let us guess that
where  ,
,  , and
, and  are, as yet, unknown exponents, and
are, as yet, unknown exponents, and  is a dimensionless constant.
Now, the dimensions of
is a dimensionless constant.
Now, the dimensions of 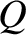 are
are ![$[L]^3/[T]$](img122.png) , the dimensions of
, the dimensions of 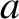 are
are ![$[L]$](img123.png) , the dimensions
of
, the dimensions
of 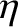 are
are
![$[M]/([L]\,[T])$](img124.png) , and the dimensions of
, and the dimensions of
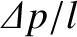 are
are
![$\{([M]\,[L]/[T]^2)/[L]^2\}/[L] = [M]/([L]^2\,[T]^2)$](img125.png) .
Thus, equating the dimensions of the left- and right-hand sides of the previous equation, we obtain
.
Thus, equating the dimensions of the left- and right-hand sides of the previous equation, we obtain
![$\displaystyle \frac{[L]^3}{[T]} = [L]^x\left(\frac{[M]}{[L]\,[T]}\right)^y\left(\frac{[M]}{[L]^2\,[T]^2}\right)^z.$](img126.png)
![$[L]$](img123.png) ,
we obtain
,
we obtain
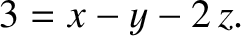
![$[M]$](img128.png) , we get
, we get
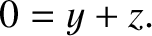
![$[T]$](img130.png) , we obtain
, we obtain
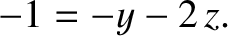
 ,
,  , and
, and 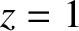 . Hence, we deduce that
. Hence, we deduce that