Next: Deriving Physical Relationships Up: Units Previous: Other Units
 is a mass and
is a mass and  is a length, cannot possibly be correct. One easy way of
seeing that Equation (1.3) is invalid (as a law of physics) is to note that this equation
is dependent on the adopted system of units. That is, if
is a length, cannot possibly be correct. One easy way of
seeing that Equation (1.3) is invalid (as a law of physics) is to note that this equation
is dependent on the adopted system of units. That is, if 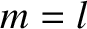 in mks units then
in mks units then
 in fps units, because the conversion factors which must be
applied to the left- and right-hand
sides of the equation differ. Physicists hold very strongly to the maxim that the laws of physics
possess objective reality. In other words, the laws of physics are equivalent for
all observers. One immediate consequence of this maxim is that a law
of physics must take the same form in all possible systems of units that a prospective
observer might choose to employ (because the choice of units is arbitrary, and has nothing to do with physical reality). The only way in which this can be the case is if
all laws of physics are dimensionally consistent. In other words, the quantities
on the left- and right-hand sides of the equality sign in any given law of
physics must have the same dimensions (i.e.,
the same combinations of length, mass, and time). A dimensionally consistent equation
naturally takes the same form in all possible systems of units, because the same conversion
factors are applied to both sides of the equation when transforming from one system to another.
in fps units, because the conversion factors which must be
applied to the left- and right-hand
sides of the equation differ. Physicists hold very strongly to the maxim that the laws of physics
possess objective reality. In other words, the laws of physics are equivalent for
all observers. One immediate consequence of this maxim is that a law
of physics must take the same form in all possible systems of units that a prospective
observer might choose to employ (because the choice of units is arbitrary, and has nothing to do with physical reality). The only way in which this can be the case is if
all laws of physics are dimensionally consistent. In other words, the quantities
on the left- and right-hand sides of the equality sign in any given law of
physics must have the same dimensions (i.e.,
the same combinations of length, mass, and time). A dimensionally consistent equation
naturally takes the same form in all possible systems of units, because the same conversion
factors are applied to both sides of the equation when transforming from one system to another.
As an example, let us consider what is probably the most famous equation in physics; that is, Einstein's mass-energy relation,
(See Section 3.3.4.) Here, is the energy of a body,
is the energy of a body,  is its mass, and
is its mass, and  is the speed of light in
vacuum. The dimensions of energy are
is the speed of light in
vacuum. The dimensions of energy are
![$[M]\,[L]^2/[T]^2$](img110.png) , and the dimensions of
speed are
, and the dimensions of
speed are ![$[L]/[T]$](img111.png) . Hence, the dimensions of the left-hand side are
. Hence, the dimensions of the left-hand side are
![$[M]\,[L]^2/[T]^2$](img110.png) , whereas the dimensions of the right-hand side are
, whereas the dimensions of the right-hand side are
![$[M]\,([L]/[T])^2= [M]\,[L]^2/[T]^2$](img112.png) . It follows that Equation (1.4) is indeed dimensionally
consistent. Thus,
. It follows that Equation (1.4) is indeed dimensionally
consistent. Thus,
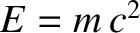 holds good in mks units, in cgs units, in fps units, and in
any other sensible
set of units. Had Einstein proposed
holds good in mks units, in cgs units, in fps units, and in
any other sensible
set of units. Had Einstein proposed 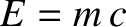 , or
, or
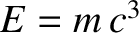 then his error would
have been immediately apparent to other physicists, because these prospective laws
are not dimensionally consistent. In fact,
then his error would
have been immediately apparent to other physicists, because these prospective laws
are not dimensionally consistent. In fact,
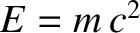 represents the only simple, dimensionally
consistent way of combining an energy, a mass, and the velocity of light in a law of
physics.
represents the only simple, dimensionally
consistent way of combining an energy, a mass, and the velocity of light in a law of
physics.
The last comment leads naturally to the subject of dimensional analysis. That is, the use of the idea of dimensional consistency to guess the forms of simple laws of physics.