Next: Newton's Laws of Motion Up: Units Previous: Deriving Physical Relationships
Although, at this stage, we do not know how to apply the laws of physics to the
problem of a tower falling over, we can, at least, make some educated guesses as to the factors
upon which the time, 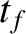 , required for this process to occur depends. In fact, it
seems reasonable to suppose that
, required for this process to occur depends. In fact, it
seems reasonable to suppose that 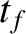 depends principally on the mass of the tower,
depends principally on the mass of the tower,  , the
height of the tower,
, the
height of the tower, 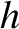 , and the acceleration due to gravity,
, and the acceleration due to gravity, 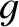 . In other words,
. In other words,
 is a dimensionless constant, and
is a dimensionless constant, and  ,
,  , and
, and  are unknown exponents. The
exponents
are unknown exponents. The
exponents  ,
,  , and
, and  can be determined by the requirement that the previous equation be dimensionally
consistent. Incidentally, the dimensions of an acceleration are
can be determined by the requirement that the previous equation be dimensionally
consistent. Incidentally, the dimensions of an acceleration are ![$[L]/[T]^2$](img140.png) . Hence,
equating the dimensions of both sides of Equation (1.11), we obtain
. Hence,
equating the dimensions of both sides of Equation (1.11), we obtain
![$\displaystyle [T] = [M]^{\,x}\,[L]^{\,y}\,\left(\frac{[L]}{[T]^2}\right)^{\,z}.$](img141.png) |
(1.12) |
![$[L]$](img123.png) ,
, ![$[M]$](img128.png) , and
, and ![$[T]$](img130.png) on either side of the
previous expression. These exponents must all match in order for Equation (1.11) to be dimensionally
consistent. Thus,
on either side of the
previous expression. These exponents must all match in order for Equation (1.11) to be dimensionally
consistent. Thus,
| 0 | 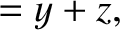 |
(1.13) |
| 0 | 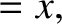 |
(1.14) |
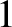 |
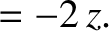 |
(1.15) |
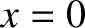 ,
, 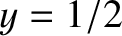 , and
, and 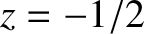 . Hence,
. Hence,
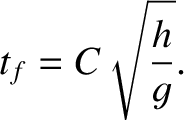 |
(1.16) |
Now, the actual tower of Pisa is approximately 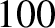 m tall. It follows that because
m tall. It follows that because
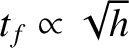 (
(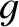 is the same for both the real and the model tower) the
1 m high model tower would fall over a factor of
is the same for both the real and the model tower) the
1 m high model tower would fall over a factor of
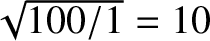 times faster than the real
tower. Thus, the film must be slowed down by a factor of 10 in order to make it look realistic.
times faster than the real
tower. Thus, the film must be slowed down by a factor of 10 in order to make it look realistic.