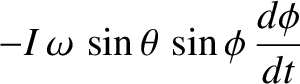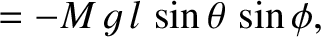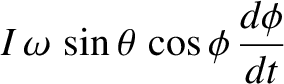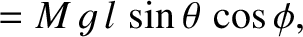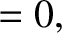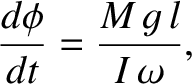Gyroscopic Precession
Consider a gyroscope that consists of a symmetric top of mass  that rotates about its symmetry axis at the
constant angular velocity
that rotates about its symmetry axis at the
constant angular velocity  . (The rotation axis is obviously a principal axis of rotation.) The top is free to rotate (without friction) about a fixed pivot point
. (The rotation axis is obviously a principal axis of rotation.) The top is free to rotate (without friction) about a fixed pivot point  . Suppose that the
axis of the top subtends a constant angle
. Suppose that the
axis of the top subtends a constant angle  with the vertical. Let us set up a Cartesian coordinate
system such that the
with the vertical. Let us set up a Cartesian coordinate
system such that the  -axis is vertical, and the
-axis is vertical, and the  -
- plane is horizontal. Suppose that the projection of
the axis of the top on to the
plane is horizontal. Suppose that the projection of
the axis of the top on to the  -
- plane subtends an (instantaneous) angle
plane subtends an (instantaneous) angle  with the
with the  -axis. Let
-axis. Let  be the
center of mass of the top (which lies on the symmetry axis), and let the distance
be the
center of mass of the top (which lies on the symmetry axis), and let the distance  be
be  . Finally,
let
. Finally,
let  be the (principal) moment of inertia of the top about its symmetry axis. See Figure 1.10.
be the (principal) moment of inertia of the top about its symmetry axis. See Figure 1.10.
Figure 1.10:
A gyroscope.
|
|
It follows, from Figure 1.10, that the angular velocity of the top is
 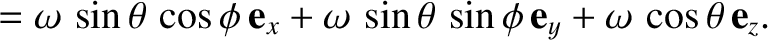 |
(1.230) |
Hence, the angular momentum of the top is
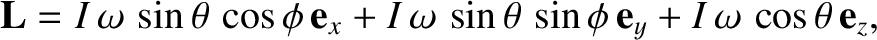 |
(1.231) |
where use has been made of Equation (1.191).
Now, the weight of the top exerts a torque
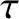 that is of magnitude
that is of magnitude
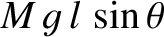 and whose direction is
specified in the figure. Here,
and whose direction is
specified in the figure. Here, 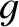 is the acceleration due to gravity. Hence,
is the acceleration due to gravity. Hence,
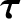 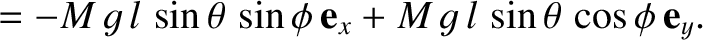 |
(1.232) |
The angular equation of motion of the top, (1.180), is
Assuming that  and
and  are constants, whereas
are constants, whereas  is time-varying,
the
is time-varying,
the  -,
-,  -, and
-, and  -components of the previous equation are
-components of the previous equation are
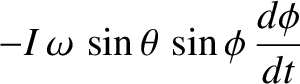 |
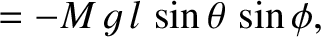 |
(1.234) |
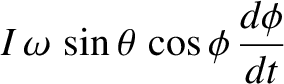 |
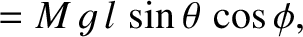 |
(1.235) |
| 0 |
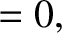 |
(1.236) |
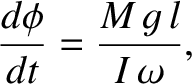 |
(1.237) |
while maintaining a constant inclination to the vertical, and a constant spin rate.
Note that the precession is in the same direction as the vertical component of the top's angular velocity. Interestingly enough, the precession rate is independent of the angle of inclination of the rotation axis to the vertical.
 that rotates about its symmetry axis at the
constant angular velocity
that rotates about its symmetry axis at the
constant angular velocity  . (The rotation axis is obviously a principal axis of rotation.) The top is free to rotate (without friction) about a fixed pivot point
. (The rotation axis is obviously a principal axis of rotation.) The top is free to rotate (without friction) about a fixed pivot point  . Suppose that the
axis of the top subtends a constant angle
. Suppose that the
axis of the top subtends a constant angle  with the vertical. Let us set up a Cartesian coordinate
system such that the
with the vertical. Let us set up a Cartesian coordinate
system such that the  -axis is vertical, and the
-axis is vertical, and the  -
- plane is horizontal. Suppose that the projection of
the axis of the top on to the
plane is horizontal. Suppose that the projection of
the axis of the top on to the  -
- plane subtends an (instantaneous) angle
plane subtends an (instantaneous) angle  with the
with the  -axis. Let
-axis. Let  be the
center of mass of the top (which lies on the symmetry axis), and let the distance
be the
center of mass of the top (which lies on the symmetry axis), and let the distance  be
be  . Finally,
let
. Finally,
let  be the (principal) moment of inertia of the top about its symmetry axis. See Figure 1.10.
be the (principal) moment of inertia of the top about its symmetry axis. See Figure 1.10.
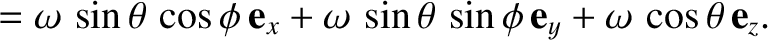
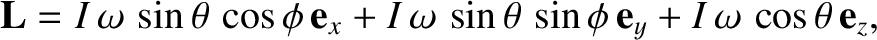
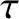 that is of magnitude
that is of magnitude
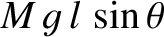 and whose direction is
specified in the figure. Here,
and whose direction is
specified in the figure. Here, 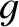 is the acceleration due to gravity. Hence,
is the acceleration due to gravity. Hence,
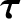

 and
and  are constants, whereas
are constants, whereas  is time-varying,
the
is time-varying,
the  -,
-,  -, and
-, and  -components of the previous equation are
-components of the previous equation are