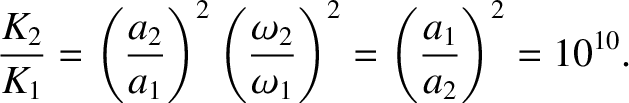A star can be thought of as a spherically symmetric body that rotates about an axis passing through its center.
The spherical symmetry of the star implies that all three of its principal moments of inertia are equal to one another,
and that any axis that passes through the center is a principal axis of rotation. (See Section 1.7.2.)
Suppose that the star in question
is rotating about the  -axis. Its moment of inertia is
-axis. Its moment of inertia is
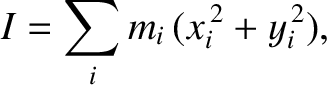 |
(1.219) |
where the sum is over all of the mass elements that make up the star. If we model the star as a body of uniform mass
density 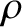 then the previous equation becomes
then the previous equation becomes
 |
(1.220) |
where 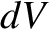 is a volume element, and the integral is over the volume of the star.
In spherical polar coordinates,
is a volume element, and the integral is over the volume of the star.
In spherical polar coordinates,
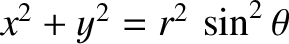 and
and
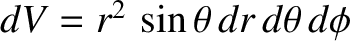 .
(See Section A.23.) Hence,
.
(See Section A.23.) Hence,
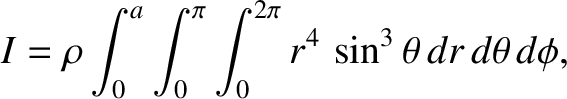 |
(1.221) |
where 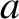 is the radius of the star. It follows that
is the radius of the star. It follows that
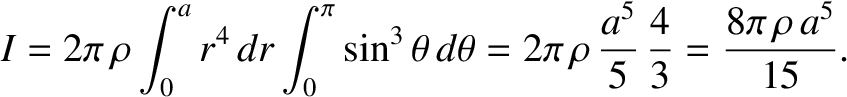 |
(1.222) |
However,
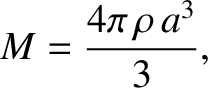 |
(1.223) |
where  is the mass of the star. The previous two equations yield
is the mass of the star. The previous two equations yield
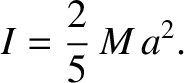 |
(1.224) |
The angular momentum of the star is
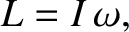 |
(1.225) |
where  is its angular velocity. If the star is isolated, such that it is not subject to an external
torque, then its angular equation of motion, (1.180), reduces to
is its angular velocity. If the star is isolated, such that it is not subject to an external
torque, then its angular equation of motion, (1.180), reduces to
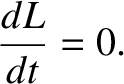 |
(1.226) |
In other words, the angular momentum of the star is a conserved quantity.
Consider what would happen if a star such as the Sun collapsed gravitationally until it became a
neutron star. The radius of the Sun-like star is about 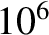 km. On the other hand, the
radius of a neutron star is only about
km. On the other hand, the
radius of a neutron star is only about 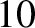 km. Moreover, the Sun rotates at about 1 revolution per month,
which corresponds to an angular velocity of
km. Moreover, the Sun rotates at about 1 revolution per month,
which corresponds to an angular velocity of
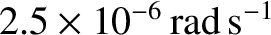 . Thus, we are considering a
process in which the star's initial radius and angular velocity are
. Thus, we are considering a
process in which the star's initial radius and angular velocity are 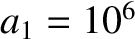 km and
km and
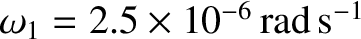 , respectively, and its final radius is
, respectively, and its final radius is 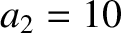 km. The question is what is the star's final angular velocity,
km. The question is what is the star's final angular velocity, 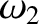 .
Well, it is clear from Equations (1.224) and (1.225) that if angular momentum is to be conserved during the
collapse then we require
.
Well, it is clear from Equations (1.224) and (1.225) that if angular momentum is to be conserved during the
collapse then we require
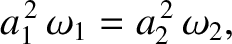 |
(1.227) |
or
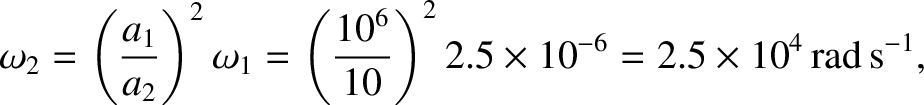 |
(1.228) |
which corresponds to about 4000 revolutions per second. Thus, we deduce that neutron stars are likely to rotate
thousands of times a second (as is indeed the case) as a consequence of the conservation of angular momentum during their formation. Finally, the star's rotational kinetic energy is
 , so
the ratio of the final to the initial kinetic energy of the star is
, so
the ratio of the final to the initial kinetic energy of the star is
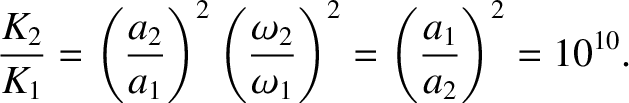 |
(1.229) |
 -axis. Its moment of inertia is
-axis. Its moment of inertia is
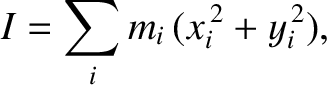
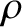 then the previous equation becomes
then the previous equation becomes

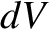 is a volume element, and the integral is over the volume of the star.
In spherical polar coordinates,
is a volume element, and the integral is over the volume of the star.
In spherical polar coordinates,
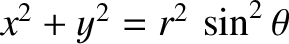 and
and
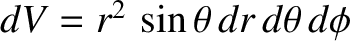 .
(See Section A.23.) Hence,
.
(See Section A.23.) Hence,
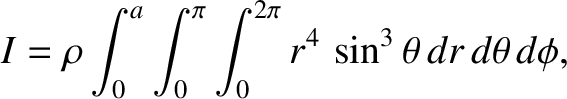
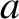 is the radius of the star. It follows that
is the radius of the star. It follows that
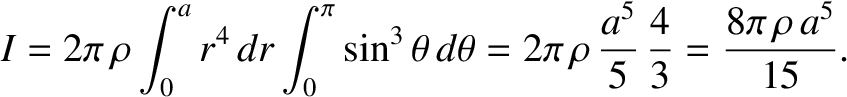
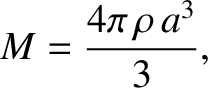
 is the mass of the star. The previous two equations yield
is the mass of the star. The previous two equations yield
 is its angular velocity. If the star is isolated, such that it is not subject to an external
torque, then its angular equation of motion, (1.180), reduces to
is its angular velocity. If the star is isolated, such that it is not subject to an external
torque, then its angular equation of motion, (1.180), reduces to
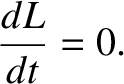
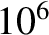 km. On the other hand, the
radius of a neutron star is only about
km. On the other hand, the
radius of a neutron star is only about 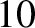 km. Moreover, the Sun rotates at about 1 revolution per month,
which corresponds to an angular velocity of
km. Moreover, the Sun rotates at about 1 revolution per month,
which corresponds to an angular velocity of
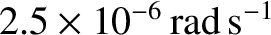 . Thus, we are considering a
process in which the star's initial radius and angular velocity are
. Thus, we are considering a
process in which the star's initial radius and angular velocity are 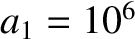 km and
km and
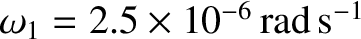 , respectively, and its final radius is
, respectively, and its final radius is 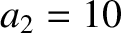 km. The question is what is the star's final angular velocity,
km. The question is what is the star's final angular velocity, 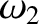 .
Well, it is clear from Equations (1.224) and (1.225) that if angular momentum is to be conserved during the
collapse then we require
.
Well, it is clear from Equations (1.224) and (1.225) that if angular momentum is to be conserved during the
collapse then we require
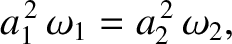
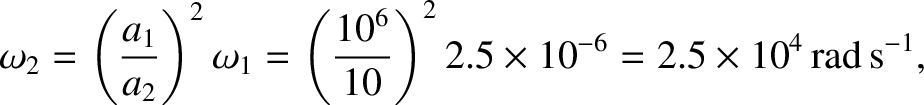
 , so
the ratio of the final to the initial kinetic energy of the star is
, so
the ratio of the final to the initial kinetic energy of the star is