Consider a particle of mass  trapped in a one-dimensional, square, potential
well of width
trapped in a one-dimensional, square, potential
well of width 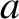 and finite depth
and finite depth 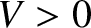 . Suppose that the potential takes the form
. Suppose that the potential takes the form
![\begin{displaymath}U(x) = \left\{
\begin{array}{rll}
-V &\mbox{\hspace{0.5cm}}&\...
...\vert\leq a/2\\ [0.5ex]
0&&\mbox{otherwise}
\end{array}\right..\end{displaymath}](img3072.png) |
(4.89) |
Here, we have adopted the standard convention that
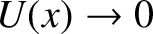 as
as
 .
This convention is useful because, just as in classical mechanics, a particle whose overall energy,
.
This convention is useful because, just as in classical mechanics, a particle whose overall energy,  ,
is negative is bound in the well (i.e., it cannot escape to infinity), whereas a
particle whose overall energy is positive is unbound. (See Section 1.3.6.) Because we are interested in bound particles,
we shall assume that
,
is negative is bound in the well (i.e., it cannot escape to infinity), whereas a
particle whose overall energy is positive is unbound. (See Section 1.3.6.) Because we are interested in bound particles,
we shall assume that 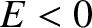 . We shall also assume that
. We shall also assume that 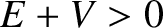 , in order to allow the particle
to have a positive kinetic energy inside the well.
, in order to allow the particle
to have a positive kinetic energy inside the well.
Let us search for a stationary state
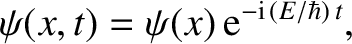 |
(4.90) |
whose stationary wavefunction, 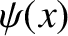 , satisfies the time-independent Schrödinger equation,
(4.71). Solutions to Equation (4.71) in the symmetric
[i.e.,
, satisfies the time-independent Schrödinger equation,
(4.71). Solutions to Equation (4.71) in the symmetric
[i.e.,
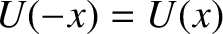 ] potential (4.89) are either totally
symmetric [i.e.,
] potential (4.89) are either totally
symmetric [i.e.,
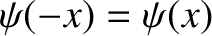 ] or totally antisymmetric [i.e.,
] or totally antisymmetric [i.e.,
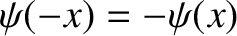 ].
Moreover, the solutions must satisfy the boundary condition
otherwise they would not correspond to bound states.
].
Moreover, the solutions must satisfy the boundary condition
otherwise they would not correspond to bound states.
Let us, first of all, search for a totally-symmetric solution. In the region to the left of the well (i.e., 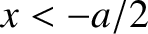 ),
the solution of the time-independent Schrödinger equation that satisfies the boundary condition
),
the solution of the time-independent Schrödinger equation that satisfies the boundary condition
 as
as
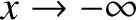 is
is
 |
(4.92) |
where
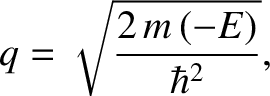 |
(4.93) |
and  is a constant. By symmetry, the solution in the region to the right of the well (i.e.,
is a constant. By symmetry, the solution in the region to the right of the well (i.e.,  )
is
)
is
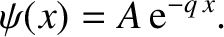 |
(4.94) |
The solution inside the well (i.e.,
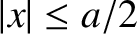 ) that satisfies the symmetry
constraint
) that satisfies the symmetry
constraint
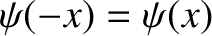 is
is
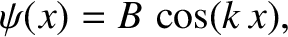 |
(4.95) |
where
 |
(4.96) |
and  is a constant.
The appropriate matching conditions at the edges of the well (i.e.,
is a constant.
The appropriate matching conditions at the edges of the well (i.e., 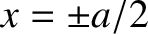 ) are that
) are that 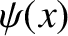 and
and
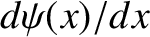 both be continuous [because a discontinuity in the
wavefunction, or its first derivative, would generate a singular term in the time-independent Schrödinger equation
(i.e., the term involving
both be continuous [because a discontinuity in the
wavefunction, or its first derivative, would generate a singular term in the time-independent Schrödinger equation
(i.e., the term involving
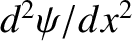 ) that could not be balanced]. The matching conditions yield
) that could not be balanced]. The matching conditions yield
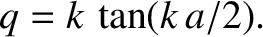 |
(4.97) |
Let  . It follows that
. It follows that
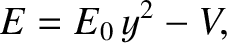 |
(4.98) |
where
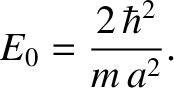 |
(4.99) |
Moreover, Equation (4.97) becomes
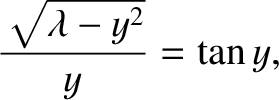 |
(4.100) |
with
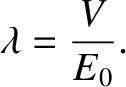 |
(4.101) |
Here,  must lie in the range
must lie in the range
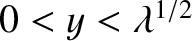 , in order to ensure that
, in order to ensure that  lies in the range
lies in the range  .
.
Figure: 4.5
The curves  (solid) and
(solid) and
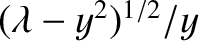 (dashed), calculated for
(dashed), calculated for
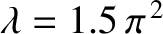 . The latter curve takes the
value 0 when
. The latter curve takes the
value 0 when
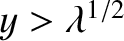 .
.
|
|
The solutions of Equation (4.100) correspond to the
intersection of the curve
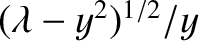 with the curve
with the curve
 . Figure 4.5 shows these two curves plotted for
a particular value of
. Figure 4.5 shows these two curves plotted for
a particular value of 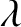 . In this case, the curves intersect
twice, indicating the existence of two totally-symmetric bound states in the well.
It is apparent, from the figure, that as
. In this case, the curves intersect
twice, indicating the existence of two totally-symmetric bound states in the well.
It is apparent, from the figure, that as 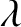 increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that there is
always at least one totally-symmetric bound state, no matter how small
increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that there is
always at least one totally-symmetric bound state, no matter how small 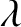 becomes (i.e., no matter how shallow the well becomes). In the limit
becomes (i.e., no matter how shallow the well becomes). In the limit
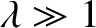 (i.e., the limit in which the well is very deep), the
solutions to Equation (4.100) asymptote to the roots of
(i.e., the limit in which the well is very deep), the
solutions to Equation (4.100) asymptote to the roots of
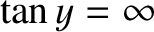 .
This gives
.
This gives
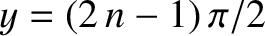 , where
, where  is a positive integer, or
is a positive integer, or
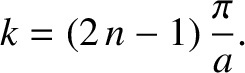 |
(4.102) |
These solutions are equivalent to the odd- infinite-depth potential well solutions
specified by Equation (4.77).
infinite-depth potential well solutions
specified by Equation (4.77).
Figure: 4.6
The curves  (solid) and
(solid) and
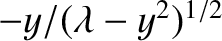 (dashed), calculated for
(dashed), calculated for
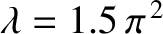 .
.
|
|
For the case of a totally-antisymmetric bound state, similar analysis to the
preceding yields
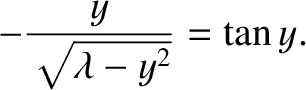 |
(4.103) |
The solutions of this equation correspond to the intersection of the
curve  with the curve
with the curve
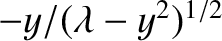 . Figure 4.6 shows these two curves plotted for
the same value of
. Figure 4.6 shows these two curves plotted for
the same value of 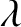 as that used in Figure 4.5. In this
case, the curves intersect once, indicating the existence of
a single totally-antisymmetric bound state in the well. It is, again, apparent, from the figure, that as
as that used in Figure 4.5. In this
case, the curves intersect once, indicating the existence of
a single totally-antisymmetric bound state in the well. It is, again, apparent, from the figure, that as 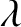 increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that
when
increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that
when 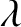 becomes sufficiently small [i.e.,
becomes sufficiently small [i.e.,
 ] then there is no totally
antisymmetric bound state. In other words, a very shallow potential well
always possesses a totally-symmetric bound state, but does not generally
possess a totally-antisymmetric bound state. In the limit
] then there is no totally
antisymmetric bound state. In other words, a very shallow potential well
always possesses a totally-symmetric bound state, but does not generally
possess a totally-antisymmetric bound state. In the limit
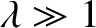 (i.e., the limit in which the well becomes very deep), the
solutions to Equation (4.103) asymptote to the roots of
(i.e., the limit in which the well becomes very deep), the
solutions to Equation (4.103) asymptote to the roots of 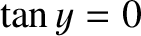 .
This gives
.
This gives
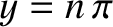 , where
, where  is a positive integer, or
is a positive integer, or
 |
(4.104) |
These solutions are equivalent to the even- infinite-depth potential well solutions
specified by Equation (4.77).
infinite-depth potential well solutions
specified by Equation (4.77).
Probably the most surprising aspect of the bound states that we have just
described is the possibility of finding the particle outside the well; that is, in the region  where
where 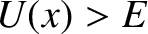 . This follows from Equation (4.94) and (4.95)
because the ratio
. This follows from Equation (4.94) and (4.95)
because the ratio
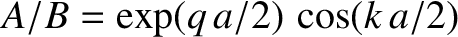 is not necessarily zero.
Such behavior is strictly forbidden
in classical mechanics, according to which a particle of energy
is not necessarily zero.
Such behavior is strictly forbidden
in classical mechanics, according to which a particle of energy  is restricted to
regions of space where
is restricted to
regions of space where  . (See Section 1.3.6.) In fact, in the case of the ground state (i.e., the lowest
energy symmetric state) it is possible to demonstrate that the probability of a
measurement finding the particle outside the well is
. (See Section 1.3.6.) In fact, in the case of the ground state (i.e., the lowest
energy symmetric state) it is possible to demonstrate that the probability of a
measurement finding the particle outside the well is
 |
(4.105) |
for a shallow well (i.e.,
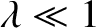 ), and
), and
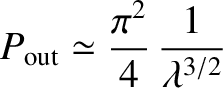 |
(4.106) |
for a deep well (i.e.,
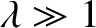 ). It follows that the particle is very likely to be found outside a shallow well, and there is a small, but finite, probability of it being found outside a deep well.
In fact, the probability of
finding the particle outside the well only goes to zero in the case of an infinitely deep well (i.e.,
). It follows that the particle is very likely to be found outside a shallow well, and there is a small, but finite, probability of it being found outside a deep well.
In fact, the probability of
finding the particle outside the well only goes to zero in the case of an infinitely deep well (i.e.,
 ).
).
 trapped in a one-dimensional, square, potential
well of width
trapped in a one-dimensional, square, potential
well of width 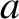 and finite depth
and finite depth 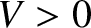 . Suppose that the potential takes the form
Here, we have adopted the standard convention that
. Suppose that the potential takes the form
Here, we have adopted the standard convention that
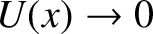 as
as
 .
This convention is useful because, just as in classical mechanics, a particle whose overall energy,
.
This convention is useful because, just as in classical mechanics, a particle whose overall energy,  ,
is negative is bound in the well (i.e., it cannot escape to infinity), whereas a
particle whose overall energy is positive is unbound. (See Section 1.3.6.) Because we are interested in bound particles,
we shall assume that
,
is negative is bound in the well (i.e., it cannot escape to infinity), whereas a
particle whose overall energy is positive is unbound. (See Section 1.3.6.) Because we are interested in bound particles,
we shall assume that 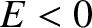 . We shall also assume that
. We shall also assume that 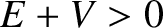 , in order to allow the particle
to have a positive kinetic energy inside the well.
, in order to allow the particle
to have a positive kinetic energy inside the well.
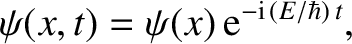
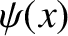 , satisfies the time-independent Schrödinger equation,
(4.71). Solutions to Equation (4.71) in the symmetric
[i.e.,
, satisfies the time-independent Schrödinger equation,
(4.71). Solutions to Equation (4.71) in the symmetric
[i.e.,
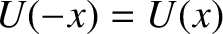 ] potential (4.89) are either totally
symmetric [i.e.,
] potential (4.89) are either totally
symmetric [i.e.,
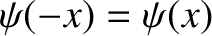 ] or totally antisymmetric [i.e.,
] or totally antisymmetric [i.e.,
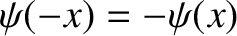 ].
Moreover, the solutions must satisfy the boundary condition
].
Moreover, the solutions must satisfy the boundary condition

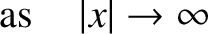
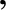
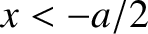 ),
the solution of the time-independent Schrödinger equation that satisfies the boundary condition
),
the solution of the time-independent Schrödinger equation that satisfies the boundary condition
 as
as
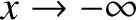 is
is

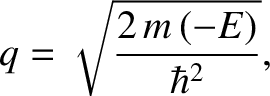
 is a constant. By symmetry, the solution in the region to the right of the well (i.e.,
is a constant. By symmetry, the solution in the region to the right of the well (i.e.,  )
is
The solution inside the well (i.e.,
)
is
The solution inside the well (i.e.,
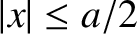 ) that satisfies the symmetry
constraint
) that satisfies the symmetry
constraint
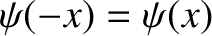 is
where
is
where

 is a constant.
The appropriate matching conditions at the edges of the well (i.e.,
is a constant.
The appropriate matching conditions at the edges of the well (i.e., 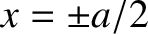 ) are that
) are that 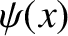 and
and
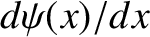 both be continuous [because a discontinuity in the
wavefunction, or its first derivative, would generate a singular term in the time-independent Schrödinger equation
(i.e., the term involving
both be continuous [because a discontinuity in the
wavefunction, or its first derivative, would generate a singular term in the time-independent Schrödinger equation
(i.e., the term involving
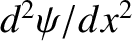 ) that could not be balanced]. The matching conditions yield
) that could not be balanced]. The matching conditions yield
 . It follows that
. It follows that
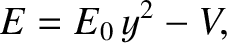
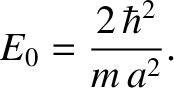
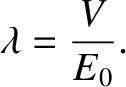
 must lie in the range
must lie in the range
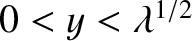 , in order to ensure that
, in order to ensure that  lies in the range
lies in the range  .
.
![\includegraphics[width=0.85\textwidth]{Chapter05/fig11_06.eps}](img3102.png)
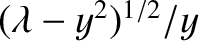 with the curve
with the curve
 . Figure 4.5 shows these two curves plotted for
a particular value of
. Figure 4.5 shows these two curves plotted for
a particular value of 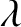 . In this case, the curves intersect
twice, indicating the existence of two totally-symmetric bound states in the well.
It is apparent, from the figure, that as
. In this case, the curves intersect
twice, indicating the existence of two totally-symmetric bound states in the well.
It is apparent, from the figure, that as 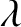 increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that there is
always at least one totally-symmetric bound state, no matter how small
increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that there is
always at least one totally-symmetric bound state, no matter how small 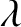 becomes (i.e., no matter how shallow the well becomes). In the limit
becomes (i.e., no matter how shallow the well becomes). In the limit
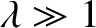 (i.e., the limit in which the well is very deep), the
solutions to Equation (4.100) asymptote to the roots of
(i.e., the limit in which the well is very deep), the
solutions to Equation (4.100) asymptote to the roots of
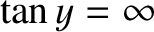 .
This gives
.
This gives
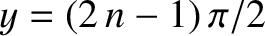 , where
, where  is a positive integer, or
is a positive integer, or
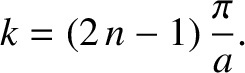
 infinite-depth potential well solutions
specified by Equation (4.77).
infinite-depth potential well solutions
specified by Equation (4.77).
 with the curve
with the curve
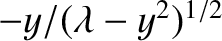 . Figure 4.6 shows these two curves plotted for
the same value of
. Figure 4.6 shows these two curves plotted for
the same value of  as that used in Figure 4.5. In this
case, the curves intersect once, indicating the existence of
a single totally-antisymmetric bound state in the well. It is, again, apparent, from the figure, that as
as that used in Figure 4.5. In this
case, the curves intersect once, indicating the existence of
a single totally-antisymmetric bound state in the well. It is, again, apparent, from the figure, that as 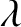 increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that
when
increases (i.e., as the well becomes
deeper) there are more and more bound states. However, it is also apparent that
when 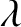 becomes sufficiently small [i.e.,
becomes sufficiently small [i.e.,
 ] then there is no totally
antisymmetric bound state. In other words, a very shallow potential well
always possesses a totally-symmetric bound state, but does not generally
possess a totally-antisymmetric bound state. In the limit
] then there is no totally
antisymmetric bound state. In other words, a very shallow potential well
always possesses a totally-symmetric bound state, but does not generally
possess a totally-antisymmetric bound state. In the limit
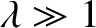 (i.e., the limit in which the well becomes very deep), the
solutions to Equation (4.103) asymptote to the roots of
(i.e., the limit in which the well becomes very deep), the
solutions to Equation (4.103) asymptote to the roots of 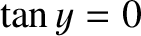 .
This gives
.
This gives
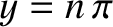 , where
, where  is a positive integer, or
is a positive integer, or

 infinite-depth potential well solutions
specified by Equation (4.77).
infinite-depth potential well solutions
specified by Equation (4.77).
 where
where 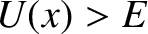 . This follows from Equation (4.94) and (4.95)
because the ratio
. This follows from Equation (4.94) and (4.95)
because the ratio
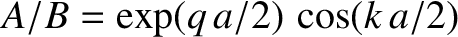 is not necessarily zero.
Such behavior is strictly forbidden
in classical mechanics, according to which a particle of energy
is not necessarily zero.
Such behavior is strictly forbidden
in classical mechanics, according to which a particle of energy  is restricted to
regions of space where
is restricted to
regions of space where  . (See Section 1.3.6.) In fact, in the case of the ground state (i.e., the lowest
energy symmetric state) it is possible to demonstrate that the probability of a
measurement finding the particle outside the well is
. (See Section 1.3.6.) In fact, in the case of the ground state (i.e., the lowest
energy symmetric state) it is possible to demonstrate that the probability of a
measurement finding the particle outside the well is

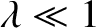 ), and
), and
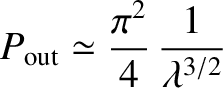
 ). It follows that the particle is very likely to be found outside a shallow well, and there is a small, but finite, probability of it being found outside a deep well.
In fact, the probability of
finding the particle outside the well only goes to zero in the case of an infinitely deep well (i.e.,
). It follows that the particle is very likely to be found outside a shallow well, and there is a small, but finite, probability of it being found outside a deep well.
In fact, the probability of
finding the particle outside the well only goes to zero in the case of an infinitely deep well (i.e.,
 ).
).