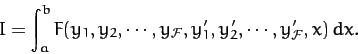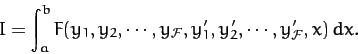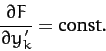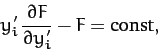Next: Hamilton's Principle
Up: Hamiltonian Dynamics
Previous: Conditional Variation
Multi-Function Variation
Suppose that we wish to maximize or minimize the functional
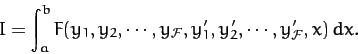 |
(707) |
Here, the integrand 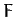 is now a functional of the
is now a functional of the 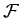 independent
functions
independent
functions 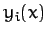 , for
, for 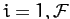 . A fairly straightforward extension of the
analysis in Section 10.2 yields
. A fairly straightforward extension of the
analysis in Section 10.2 yields 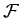 separate Euler-Lagrange equations,
separate Euler-Lagrange equations,
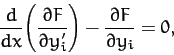 |
(708) |
for 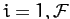 , which determine the
, which determine the 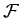 functions
functions 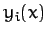 . If
. If 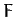 does not
explicitly depend on the function
does not
explicitly depend on the function 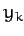 then the
then the 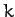 th Euler-Lagrange
equation simplifies to
th Euler-Lagrange
equation simplifies to
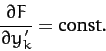 |
(709) |
Likewise, if 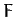 does not explicitly depend on
does not explicitly depend on 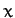 then all
then all 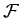 Euler-Lagrange equations simplify to
Euler-Lagrange equations simplify to
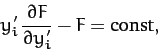 |
(710) |
for 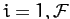 .
.
Richard Fitzpatrick
2011-03-31