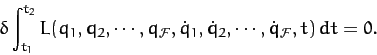Next: Constrained Lagrangian Dynamics
Up: Hamiltonian Dynamics
Previous: Multi-Function Variation
We saw, in Chapter 9, that we can specify the instantaneous configuration of a conservative dynamical system
with 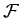 degrees of freedom in terms of
degrees of freedom in terms of 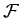 independent generalized coordinates
independent generalized coordinates 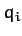 , for
, for
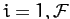 . Let
. Let
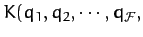
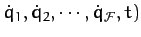 and
and
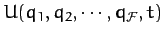 represent the kinetic and potential energies of the
system, respectively, expressed in terms of these generalized coordinates.
Here,
represent the kinetic and potential energies of the
system, respectively, expressed in terms of these generalized coordinates.
Here,
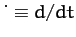 .
The Lagrangian of the system is defined
.
The Lagrangian of the system is defined
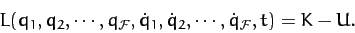 |
(711) |
Finally, the  Lagrangian equations of motion of the system take the form
Lagrangian equations of motion of the system take the form
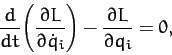 |
(712) |
for 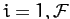 .
.
Note that the above equations of motion have exactly the same mathematical form as the Euler-Lagrange equations (708). Indeed, it is clear, from Section 10.4, that the 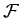 Lagrangian equations of motion (712)
can all be derived from a single equation: namely,
Lagrangian equations of motion (712)
can all be derived from a single equation: namely,
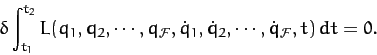 |
(713) |
In other words, the motion of the system in a given time interval is such as to maximize or
minimize the time integral of the Lagrangian, which is known as the
action integral. Thus, the laws of Newtonian dynamics can be summarized in a
single statement:
The motion of a dynamical
system in a given time interval is such as to maximize or minimize the action integral.
(In practice, the action integral is almost always minimized.) This statement is known as Hamilton's principle, and was first formulated in 1834 by the Irish
mathematician William Hamilton.



Next: Constrained Lagrangian Dynamics
Up: Hamiltonian Dynamics
Previous: Multi-Function Variation
Richard Fitzpatrick
2011-03-31
![]() Lagrangian equations of motion (712)
can all be derived from a single equation: namely,
Lagrangian equations of motion (712)
can all be derived from a single equation: namely,