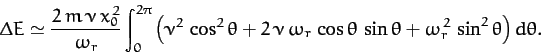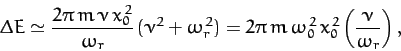Next: Resonance
Up: One-Dimensional Motion
Previous: Damped Oscillatory Motion
Quality Factor
The total energy of a damped oscillator is the sum of its kinetic and
potential energies: i.e.,
 |
(94) |
Differentiating the above expression with
respect to time, we obtain
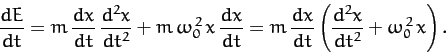 |
(95) |
It follows from Equation (83) that
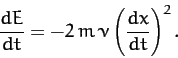 |
(96) |
We conclude that the presence of damping causes the oscillator energy to
decrease monotonically in time, and, hence, causes the amplitude of the oscillation to eventually become negligibly small [see Equation (81)].
The energy loss rate of a weakly damped (i.e.,
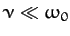 ) oscillator is conveniently
characterized in terms of a parameter,
) oscillator is conveniently
characterized in terms of a parameter, 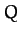 , which is known as the
quality factor. This parameter is defined to be
, which is known as the
quality factor. This parameter is defined to be  times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and
times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and 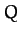 is therefore
much larger than unity. Roughly speaking,
is therefore
much larger than unity. Roughly speaking, 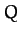 is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value.
Let us find an expression for
is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value.
Let us find an expression for 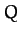 .
.
Now, the most general solution for a weakly damped
oscillator can be written in the form
[cf., Equation (91)]
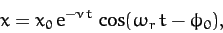 |
(97) |
where 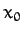 and
and  are constants, and
are constants, and
 . It follows that
. It follows that
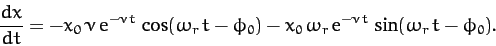 |
(98) |
Thus, making use of Equation (96), the energy lost during a single oscillation period is
where
 .
In the weakly damped limit,
.
In the weakly damped limit,
 , the exponential factor is approximately
unity in the interval
, the exponential factor is approximately
unity in the interval  to
to 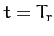 , so that
, so that
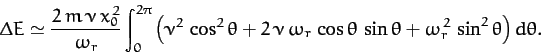 |
(100) |
Thus,
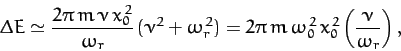 |
(101) |
since  and
and 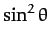 both have the average values
both have the average values 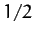 in the interval
in the interval
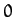 to
to  , whereas
, whereas
 has the average value
has the average value 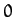 .
According to Equation (81), the energy stored in the oscillator
(at
.
According to Equation (81), the energy stored in the oscillator
(at  ) is
) is
 |
(102) |
It follows that
 |
(103) |



Next: Resonance
Up: One-Dimensional Motion
Previous: Damped Oscillatory Motion
Richard Fitzpatrick
2011-03-31


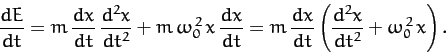
![]() ) oscillator is conveniently
characterized in terms of a parameter,
) oscillator is conveniently
characterized in terms of a parameter, ![]() , which is known as the
quality factor. This parameter is defined to be
, which is known as the
quality factor. This parameter is defined to be ![]() times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and
times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and ![]() is therefore
much larger than unity. Roughly speaking,
is therefore
much larger than unity. Roughly speaking, ![]() is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value.
Let us find an expression for
is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value.
Let us find an expression for ![]() .
.
 . It follows that
. It follows that
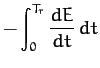
![$\displaystyle 2\,m\,\nu\,x_0^{\,2}\int_0^{T_r}{\rm e}^{-2\,\nu\,t}\left[\nu\,\cos(\omega_r\,t-\phi_0) + \omega_r\,\sin(\omega_r\,t-\phi_0)\right]^2 dt,$](img350.png)