


Next: Quality Factor
Up: One-Dimensional Motion
Previous: Simple Harmonic Motion
Damped Oscillatory Motion
According to Equation (78), a one-dimensional conservative system which is
slightly perturbed from a stable equilibrium point (and then left alone) oscillates about this
point with a fixed frequency and a constant amplitude. In other words,
the oscillations never die away. This is not very realistic, since we
know that, in practice, if we slightly perturb a dynamical system (such as a
pendulum) from a stable equilibrium point then it will indeed oscillate about this point,
but these oscillations will eventually die away due to frictional effects,
which are present in virtually all real dynamical systems. In order to model
this process, we need to include some sort of frictional drag force in
our perturbed equation of motion, (77).
The most common model for a frictional drag force is one which is
always directed in the opposite direction to the instantaneous velocity
of the object upon which it acts, and is directly proportional to the magnitude
of this velocity. Let us adopt this model.
So, our drag force can be written
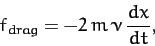 |
(82) |
where 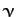 is a positive constant with the dimensions of frequency. Including such a force in our
perturbed equation of motion, (77), we obtain
is a positive constant with the dimensions of frequency. Including such a force in our
perturbed equation of motion, (77), we obtain
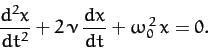 |
(83) |
Thus, the positive constant 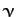 parameterizes the strength of the frictional
damping in our dynamical system.
parameterizes the strength of the frictional
damping in our dynamical system.
Equation (83) is a linear second-order ordinary differential
equation, which we suspect possesses oscillatory solutions. There is
a standard trick for solving such an equation. We search for complex
solutions of the form
 |
(84) |
where the constants 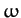 and
and 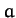 are both, in general, complex. Of course,
the physical solution is the real part of the above expression: i.e.,
are both, in general, complex. Of course,
the physical solution is the real part of the above expression: i.e.,
![\begin{displaymath}
x = \vert a\vert\,\cos[{\rm arg}(a)-{\rm Re}(\omega)\,t]\,{\rm e}^{\,{\rm Im}(\omega)\,t}.
\end{displaymath}](img312.png) |
(85) |
Clearly, the modulus and argument of the complex amplitude, 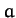 , determine
the amplitude (at
, determine
the amplitude (at  ) and phase of the oscillation, respectively, whereas the
real and imaginary parts of the complex frequency,
) and phase of the oscillation, respectively, whereas the
real and imaginary parts of the complex frequency, 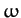 , determine its
frequency and growth-rate, respectively.
Note that this method of solution is only appropriate for linear differential
equations. Incidentally, the method works because
, determine its
frequency and growth-rate, respectively.
Note that this method of solution is only appropriate for linear differential
equations. Incidentally, the method works because
![\begin{displaymath}
{\rm Re}[{\cal L}(x)]\equiv {\cal L}({\rm Re}[x]),
\end{displaymath}](img313.png) |
(86) |
where 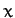 is a complex variable, and
is a complex variable, and 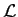 some real linear differential
operator which acts on this variable. [A linear operator satisfies
some real linear differential
operator which acts on this variable. [A linear operator satisfies
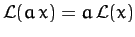 for all
for all 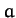 and
and 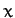 , where
, where 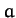 is a constant. The differential operator appearing
in Equation (83) is clearly of this type.]
is a constant. The differential operator appearing
in Equation (83) is clearly of this type.]
Substituting Equation (84) into Equation (83), we obtain
![\begin{displaymath}
a \left[-\omega^2-{\rm i}\,2\,\nu\,\omega + \omega_0^{\,2}\right]
{\rm e}^{-{\rm i}\,\omega\,t} = 0,
\end{displaymath}](img316.png) |
(87) |
which reduces to the following quadratic equation for 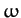 [since
[since
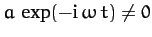 ]:
]:
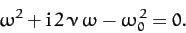 |
(88) |
The solution to this equation is
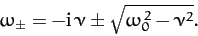 |
(89) |
Thus, the most general physical solution to Equation (83) is
![\begin{displaymath}
x(t) = {\rm Re}\left[a_+\,{\rm e}^{-{\rm i}\,\omega_+\,t}
+ a_-\,{\rm e}^{-{\rm i}\,\omega_-\,t}\right],
\end{displaymath}](img320.png) |
(90) |
where 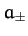 are two arbitrary complex constants.
are two arbitrary complex constants.
We can distinguish three different cases. In the first case,
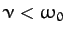 , and the motion is said to be underdamped. The most general
solution is written
, and the motion is said to be underdamped. The most general
solution is written
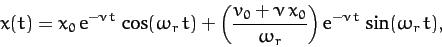 |
(91) |
where
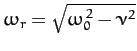 ,
, 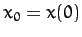 , and
, and
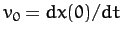 . It can be seen that the solution oscillates at some real
frequency,
. It can be seen that the solution oscillates at some real
frequency, 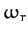 , which is somewhat less than the natural frequency
of oscillation of the undamped system,
, which is somewhat less than the natural frequency
of oscillation of the undamped system, 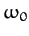 , but also decays
exponentially in time at a rate proportional to the damping coefficient,
, but also decays
exponentially in time at a rate proportional to the damping coefficient, 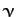 .
.
In the second case, 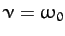 , and the motion is said to be critically damped. The most general solution is written
, and the motion is said to be critically damped. The most general solution is written
![\begin{displaymath}
x(t) = \left[x_0 \,(1+\omega_0\,t) + v_0\,t\right] {\rm e}^{-\omega_0\,t}.
\end{displaymath}](img329.png) |
(92) |
It can be seen that the solution now decays without oscillating.
In the third case, 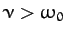 , and the motion is said to be overdamped. The most general solution is written
, and the motion is said to be overdamped. The most general solution is written
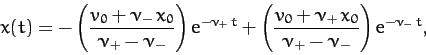 |
(93) |
where
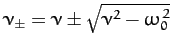 . It can be seen
that the solution again decays without oscillating, except there are now
two independent decay rates. The largest,
. It can be seen
that the solution again decays without oscillating, except there are now
two independent decay rates. The largest, 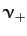 , is always greater than the
critically damped decay rate,
, is always greater than the
critically damped decay rate, 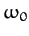 , whereas the smaller,
, whereas the smaller, 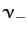 ,
is always less than this decay rate. This means that, in general,
the critically damped solution is more rapidly damped than either
the underdamped or overdamped solutions.
,
is always less than this decay rate. This means that, in general,
the critically damped solution is more rapidly damped than either
the underdamped or overdamped solutions.
Figure 5:
Damped oscillatory motion.
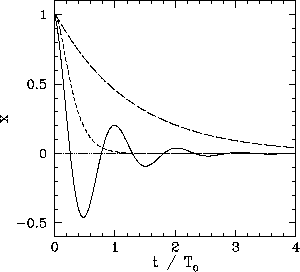 |
Figure 5 shows typical examples of underdamped (i.e.,
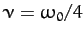 ), critically damped (i.e.,
), critically damped (i.e., 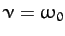 ), and
overdamped (i.e.,
), and
overdamped (i.e.,
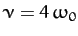 ) solutions, calculated with the
initial conditions
) solutions, calculated with the
initial conditions 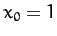 and
and 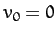 . Here,
. Here,
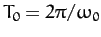 .
The three solutions correspond to the solid, short-dashed, and long-dashed curves,
respectively.
.
The three solutions correspond to the solid, short-dashed, and long-dashed curves,
respectively.



Next: Quality Factor
Up: One-Dimensional Motion
Previous: Simple Harmonic Motion
Richard Fitzpatrick
2011-03-31
![]() , and the motion is said to be underdamped. The most general
solution is written
, and the motion is said to be underdamped. The most general
solution is written
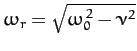 ,
, ![]() , and the motion is said to be critically damped. The most general solution is written
, and the motion is said to be critically damped. The most general solution is written
![]() , and the motion is said to be overdamped. The most general solution is written
, and the motion is said to be overdamped. The most general solution is written
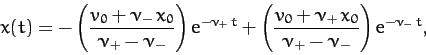
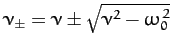 . It can be seen
that the solution again decays without oscillating, except there are now
two independent decay rates. The largest,
. It can be seen
that the solution again decays without oscillating, except there are now
two independent decay rates. The largest, ![]() ), critically damped (i.e.,
), critically damped (i.e., ![]() ), and
overdamped (i.e.,
), and
overdamped (i.e.,
![]() ) solutions, calculated with the
initial conditions
) solutions, calculated with the
initial conditions ![]() and
and ![]() . Here,
. Here,
![]() .
The three solutions correspond to the solid, short-dashed, and long-dashed curves,
respectively.
.
The three solutions correspond to the solid, short-dashed, and long-dashed curves,
respectively.