- ...Principa.
![[*]](footnote.png)
- An excellent discussion of the historical
development of Newtonian dynamics, as well as the physical and
philosophical assumptions which underpin this theory, is
given in The Discovery of Dynamics: A Study from a Machian Point of View of the Discovery and the Structure of Dynamical Theories, J.B. Barbour (Oxford University Press, Oxford UK, 2001).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tensor.
![[*]](footnote.png)
- A tensor is the two-dimensional generalization of a vector. However, for present purposes, we can
simply think of a tensor as another name for a matrix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radius.
![[*]](footnote.png)
- M.G. Stewart, American Jou. Physics 73, 730 (2005).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... years.
![[*]](footnote.png)
- Note that this precession rate is about
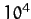 times greater than any of the planetary perihelion precession
rates discussed in Section 12.12.
times greater than any of the planetary perihelion precession
rates discussed in Section 12.12.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dynamics.
![[*]](footnote.png)
- For more information on lunar theory, see An Elementary Treatise on the Lunar Theory, H. Godfray (Macmillan & Co., 1853); An Introductory Treatise on the Lunar Theory, E.W. Brown (Cambridge University Press, 1896); Lectures on the Lunar Theory, J.C. Adams (Cambridge University Press, 1900).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... month,
![[*]](footnote.png)
- A
synodic month, which is
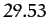 days, is the mean period between successive new moons.
days, is the mean period between successive new moons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scheme.
![[*]](footnote.png)
- W.H. Press, S.A. Teukolsky,
W.T. Vetterling, and B.P. Flannery, Numerical recipes in C: The
art of scientific computing, 2nd Edition (Cambridge University Press,
Cambridge UK, 1992), Section 16.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively.
![[*]](footnote.png)
- G.L. Baker, Control of
the chaotic driven pendulum, Am. J. Phys. 63, 832 (1995).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interactions.
![[*]](footnote.png)
- E.S. Albers
and B.W. Lee, Phys. Rep. 9C, 1 (1973).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... universe.
![[*]](footnote.png)
- P. Coles, and F. Lucchin, Cosmology: The origin and evolution
of cosmic structure, (J. Wiley & Sons, Chichester UK, 1995).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fractal.
![[*]](footnote.png)
- B.B. Mandelbrot, The fractal geometry of nature, (W.H. Freeman,
New York NY, 1982).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bifurcations.
![[*]](footnote.png)
- M.J. Feigenbaum, Quantitative universality for a
class of nonlinear transformations, J. Stat. Phys. 19, 25 (1978).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bifurcations.
![[*]](footnote.png)
- M.J. Feigenbaum,
The universal metric properties of nonlinear transformations,
J. Stat. Phys. 21, 69 (1979).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
systems.
![[*]](footnote.png)
- P. Citanovic, Universality in chaos, (Adam Hilger,
Bristol UK, 1989).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ground.
![[*]](footnote.png)
- E. Lorenz, Deterministic nonperiodic flow, J. Atmospheric
Science 20, 130 (1963).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... increased.
![[*]](footnote.png)
- N. Metropolis,
M.L. Stein, and P.R. Stein, On finite limit sets for transformations
on the unit interval, J. Combin. Theor. 15, 25 (1973).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... systems.
![[*]](footnote.png)
- R.H. Simoyi,
A. Wolf, and H.L. Swinney, One-dimensional dynamics in a multi-component
chemical reaction, Phys. Rev. Lett. 49, 245 (1982).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)